- ...
machine.1.1
- Of course, having infinitely long tape seems
impossible in the physical world. Other versions of Turing machines
exist in which the tape is finite but as long as necessary to process
the given input. This may be more appropriate for the discussion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
computation.1.2
- Performing computations with mechanical systems
is discussed in [815]. Computation models over the reals
are covered in [118].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...optimal2.1
- As in optimization literature, we will use
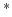 to mean optimal.
to mean optimal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....2.2
- In some variations, the vertex could be
added without a corresponding edge. This would start another tree in
a multiple-tree approach
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... iteration,2.3
- The ``value'' here refers to
the optimal cost-to-go or cost-to-come. Therefore, an alternative
name could be cost-to-go iteration.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... literals2.4
- The pair of literals need not be a complementary
pair, as defined in Section 2.4.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
conjunction2.5
- Conjunction means logical AND.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... contains3.1
- In this section,
we want the resulting set to include all of the points along the
boundary. Therefore,
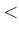 is used to model a set for removal, as
opposed to
is used to model a set for removal, as
opposed to 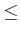 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... primitives.3.2
- An alternative that yields the same
expressive power is to still use
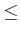 , but allow set complements, in
addition to unions and intersections.
, but allow set complements, in
addition to unions and intersections.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... frame.3.3
- The world
frame serves the same purpose as an inertial frame in Newtonian
mechanics. Intuitively, it is a frame that remains fixed and from
which all measurements are taken. See Section 13.3.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...placing3.4
- Technically, this placement is a function called an
orientation-preserving isometric embedding.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
balls.4.1
- Such a collection of balls is often referred to as a
basis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... graph4.2
- In
topology this is called a 1-complex [439].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... theory.4.3
- Technically, the images of the topological
graphs, as subspaces of
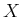 , are homeomorphic, not the graphs
themselves.
, are homeomorphic, not the graphs
themselves.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...manifold4.4
- Manifolds that are not subsets of
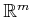 may
also be defined. This requires that
may
also be defined. This requires that 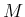 is a Hausdorff space and is
second countable, which means that there is a countable number of open
sets from which any other open set can be constructed by taking a
union of some of them. These conditions are automatically satisfied
when assuming
is a Hausdorff space and is
second countable, which means that there is a countable number of open
sets from which any other open set can be constructed by taking a
union of some of them. These conditions are automatically satisfied
when assuming
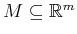 ; thus, it avoids these extra
complications and is still general enough for our purposes. Some
authors use the term manifold to refer to a smooth
manifold. This requires the definition of a smooth structure, and
the homeomorphism is replaced by diffeomorphism. This extra structure
is not needed here but will be introduced when it is needed in
Section 8.3.
; thus, it avoids these extra
complications and is still general enough for our purposes. Some
authors use the term manifold to refer to a smooth
manifold. This requires the definition of a smooth structure, and
the homeomorphism is replaced by diffeomorphism. This extra structure
is not needed here but will be introduced when it is needed in
Section 8.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... manifold.4.5
- One variant of the theorem is that
for smooth manifolds,
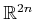 is sufficient. This bound is tight
because
is sufficient. This bound is tight
because
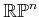 (
(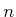 -dimensional projective space, which will be introduced
later in this section), cannot be embedded in
-dimensional projective space, which will be introduced
later in this section), cannot be embedded in
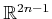 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distinct.4.6
- This is usually defined
more formally and called a quotient topology.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
happen,4.7
- The topologist's sine curve is not a manifold because
all open sets that contain the point
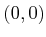 contain some of the
points from the sine curve. These open sets are not homeomorphic to
contain some of the
points from the sine curve. These open sets are not homeomorphic to
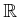 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... space.4.8
- The groups considered in
this section are actually Lie groups because they are smooth manifolds
[63]. We will not use that name here, however, because the
notion of a smooth structure has not yet been defined. Readers
familiar with Lie groups, however, will recognize most of the coming
concepts. Some details on Lie groups appear later in
Sections 15.4.3 and 15.5.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...eqn:quatmat).4.9
- Since that function was two-to-one, it
is technically not an inverse until the quaternions are restricted to
the upper hemisphere, as described previously.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... difference4.10
- In some
contexts, which include mathematics and image processing, the
Minkowski difference or Minkowski subtraction is defined
differently (instead, it is a kind of ``erosion''). For this reason,
some authors prefer to define all operations in terms of the Minkowski
sum,
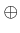 , which is consistently defined in all contexts.
Following this convention, we would define
, which is consistently defined in all contexts.
Following this convention, we would define
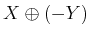 , which is
equivalent to
, which is
equivalent to
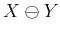 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
nicely.4.11
- This is called a Whitney stratification
[173,968].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... space.5.1
- Some
topological spaces are not metrizable, which means that no function exists that satisfies
the axioms. Many metrization theorems give sufficient conditions for
a topological space to be metrizable [451], and virtually
any space that has arisen in motion planning will be metrizable.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... measure5.2
- Such a measure is
unique up to scale and exists for any locally compact topological
group [346,836].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... random,5.3
- See Section
9.1.2 for a review of probability theory.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
random.5.4
- The directions will be formalized in Section
8.3.2 when smooth manifolds are introduced. In that case,
the directions correspond to the set of possible velocities that have
unit magnitude. Presently, the notion of a direction is only given
informally.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... random.5.5
- There are exceptions, which use physical
phenomena as a random source [808].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...dispersion5.6
- The definition is unfortunately backward
from intuition. Lower dispersion means that the points are nicely
dispersed. Thus, more dispersion is bad, which is counterintuitive.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is5.7
- The
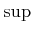 represents the supremum, which is the
least upper bound. If
represents the supremum, which is the
least upper bound. If 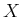 is closed, then the
is closed, then the 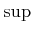 becomes a
becomes a 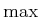 .
See Section 9.1.1 for more details.
.
See Section 9.1.1 for more details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
direction5.8
- To formally talk about directions, it would be
better to define a differentiable structure on
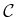 . This will be
deferred to Section 8.3, where it seems unavoidable.
. This will be
deferred to Section 8.3, where it seems unavoidable.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... trap5.9
- This principle is
actually used in real life to trap flying bugs. This analogy was
suggested by James O'Brien in a discussion with James Kuffner.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... form5.10
- Alternatively, the general lattice
definition in (5.21) could be used.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nearly5.11
- It is not constant because
the running time is proportional to the inverse Ackerman function,
which grows very, very slowly. For all practical purposes, the
algorithm operates in constant time. See Section 6.5.2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bowl.5.12
- Of course, that problem does not
appear to need so many points per axis; fewer may be used instead, if
the algorithm can adapt the sampling resolution or dispersion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... algorithms.5.13
- The exciting results obtained by the
method even helped inspire me many years ago to work on motion
planning.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
tuning.5.14
- The original RRT [598] was introduced with a
step size parameter, but this is eliminated in the current
presentation. For implementation purposes, one might still want to
revert to this older way of formulating the algorithm because the
implementation is a little easier. This will be discussed shortly.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... behavior.5.15
- If
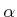 is uniform, random, then a stochastic fractal
[586] is obtained. Deterministic fractals can be
constructed using sequences that have appropriate symmetries.
is uniform, random, then a stochastic fractal
[586] is obtained. Deterministic fractals can be
constructed using sequences that have appropriate symmetries.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
PSPACE-hard6.1
- This implies NP-hard. An overview of such
complexity statements appears in Section 6.5.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... simple6.2
- A polygonal region
that has no holes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
advance.6.3
- Exceptions to this are some algorithms mentioned in
Section 6.5.3, which obtain greater efficiency by only
maintaining one connected component of
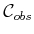 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... collision-free.6.4
- This is the reason why the approach is
defined differently from Chapter 1 of [588]. In that case,
sample points were not placed in the interiors of the 2-cells, and
collision could result for some queries.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
independent6.5
- Form
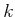 vectors by subtracting
vectors by subtracting 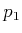 from the
other
from the
other 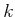 points for some positive integer
points for some positive integer 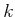 such that
such that 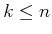 .
Arrange the vectors into a
.
Arrange the vectors into a
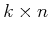 matrix. For linear
independence, there must be at least one
matrix. For linear
independence, there must be at least one
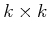 cofactor with a
nonzero determinant. For example, if
cofactor with a
nonzero determinant. For example, if 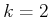 , then the three points
cannot be collinear.
, then the three points
cannot be collinear.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... polynomials6.6
- It will be
explained shortly why
![$ {\mathbb{Q}}[x_1,\ldots, x_n]$](img2243.gif) is preferred over
is preferred over
![$ {\mathbb{R}}[x_1,\ldots, x_n]$](img2244.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time.6.7
- Note that this definition may be
absurd in practice; an algorithm that runs in time
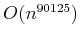 would probably not be too efficient for most purposes.
would probably not be too efficient for most purposes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... etc.).6.8
- If
you remember hearing that a planning problem is NP-something, but
cannot remember whether it was NP-hard or NP-complete, then it is safe
to say NP-hard because NP-complete implies NP-hard. This can
similarly be said for other classes, such as PSPACE-complete
vs. PSPACE-hard.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Sha046.9
- The following asymptotic notion is used:
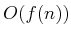 denotes an upper bound,
denotes an upper bound,
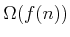 denotes a lower
bound, and
denotes a lower
bound, and
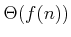 means that the bound is tight (both upper
and lower). This notation is used in most books on algorithms
[243].
means that the bound is tight (both upper
and lower). This notation is used in most books on algorithms
[243].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....6.10
- It may seem
odd for
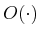 to appear in the middle of an expression. In this
context, it means that there exists some
to appear in the middle of an expression. In this
context, it means that there exists some
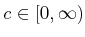 such that
the running time is bounded by
such that
the running time is bounded by
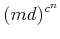 . Note that another
. Note that another 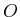 is
not necessary in front of the whole formula.
is
not necessary in front of the whole formula.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... necessary.7.1
- The
infinite acceleration and unbounded speed assumptions may annoy those
with mechanics and control backgrounds. In this case, assume that the
present models approximate the case in which every body moves slowly,
and the dynamics can be consequently neglected. If this is still not
satisfying, then jump ahead to Part IV, where general
nonlinear systems are considered. It is still helpful to consider the
implications derived from the concepts in this chapter because the
issues remain for more complicated problems that involve dynamics.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...portiernia,7.2
- This is a place where people guard the
keys at some public facilities in Poland.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
plane7.3
- Tangent planes are defined rigorously in Section
8.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
stopped.7.4
- This model allows infinite acceleration. Imagine
that the speeds are slow enough to allow this approximation. If this
is still not satisfactory, then jump ahead to Chapter 13.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
constraints.8.1
- Section 8.4.4 will actually
consider some simple differential constraints, such as acceleration
bounds; the full treatment of differential constraints is deferred
until Part IV.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
function.8.2
- This term was developed for continuous
configuration spaces in
[541,829]; it will be used
more broadly in this book but still retains the basic idea.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
space.8.3
- Difficulty in distinguishing between these two caused
researchers for many years to believe that grids yield terrible
performance for the open-loop path planning problems of Chapter
5. This was mainly because it was assumed that a
high-resolution grid was necessary. For many problems, however, they
could terminate early after only considering a few points per axis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... field8.4
- Unfortunately, the term field
appears in two unrelated places: in the definition of a vector space
and in the term vector field. Keep in mind that this is an
accidental collision of terms.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... structure8.5
- Alternative
names are differentiable structure and
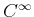 structure.
structure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
family8.6
- In literature in which the coordinate neighborhoods
are called charts, this family is called an atlas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... them.8.7
- This is under the
assumption that
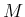 is Hausdorff and has a countable basis of open
sets, which applies to the manifolds considered here.
is Hausdorff and has a countable basis of open
sets, which applies to the manifolds considered here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
manifold.8.8
- Alternative names are differentiable
manifold and
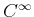 manifold.
manifold.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...sec:defbmp.8.9
- Note that
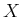 already excludes the obstacle
region. For some problems in Part IV, the state space will
be
already excludes the obstacle
region. For some problems in Part IV, the state space will
be
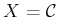 , which includes the obstacle region.
, which includes the obstacle region.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... state.8.10
- This allows
discontinuous changes in velocity, which is unrealistic in many
applications. Additional constraints, such as imposing acceleration
bounds, will also be discussed. For a complete treatment of
differential constraints, see Part IV.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time.8.11
- This is possible in finite time, even if
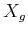 is a single point, because the vector field is not continuous.
Otherwise, only asymptotic convergence may be possible.
is a single point, because the vector field is not continuous.
Otherwise, only asymptotic convergence may be possible.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... connectivity.8.12
- This precludes a
choice of
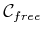 for which adding the boundary point enables a
homotopically distinct path to be made through the boundary point. An
example of this is when two square obstacles in
for which adding the boundary point enables a
homotopically distinct path to be made through the boundary point. An
example of this is when two square obstacles in
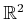 contact each
other only at a pair of corners.
contact each
other only at a pair of corners.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
definite,8.13
- Positive definite for an
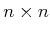 matrix
matrix 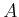 means that for all
means that for all
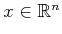 ,
,
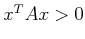 . If
. If 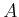 is symmetric
(which applies to
is symmetric
(which applies to 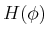 ), then this is equivalent to
), then this is equivalent to 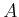 having
all positive eigenvalues.
having
all positive eigenvalues.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
definite,8.14
- Negative definite means that for all
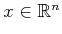 ,
,
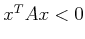 . If
. If 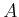 is symmetric, then this is equivalent to
is symmetric, then this is equivalent to 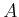 having all negative eigenvalues.
having all negative eigenvalues.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....8.15
- Some authors do not include the global minimum as a
local minimum. In this case, one would say that there are no local
minima.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... degenerate.8.16
- Technically, to be Morse, the values
of the function must also be distinct at each critical point.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variable9.1
- This is a terrible name, which often
causes confusion. A random variable is not ``random,'' nor is it a
``variable.'' It is simply a function,
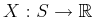 . To
make matters worse, a capital letter is usually used to denote it,
whereas lowercase letters are usually used to denote functions.
. To
make matters worse, a capital letter is usually used to denote it,
whereas lowercase letters are usually used to denote functions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... then9.2
- Using the language of measure
theory, both definitions are just special cases of the Lebesgue
integral. Measure theory nicely unifies discrete and continuous
probability theory, thereby avoiding the specification of separate
cases. See [346,546,836].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
space).9.3
- Alternatively, a random variable may be defined over
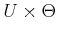 , and conditional expectation would be taken, in which
, and conditional expectation would be taken, in which
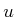 is given.
is given.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matrices.9.4
- If you enjoy
working with tensors, these could be used to capture
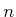 -player cost
functions [107].
-player cost
functions [107].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... outcomes.9.5
- In most utility theory
literature, this is referred to as a reward space,
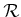 [89].
[89].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...:9.6
- Alternative
axiom systems exist [268,839].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... transitive.9.7
- For some
reasonable problems, however, transitivity is not desirable. See the
Candorcet and Simpson paradoxes in [831].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
reward.9.8
- Some axiom systems allow infinite rewards, which lead
to utility and cost functions with infinite values, but this is not
considered here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... practice.9.9
- A locally compact topological
group is required [346,836].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distributions.9.10
- Readers familiar with the
movie The Princess Bride may remember the humorous dialog
between Vizzini and the Dread Pirate Roberts about which goblet
contains the deadly Iocane powder.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ``Doh!''9.11
- In 2001, the
Homer Simpson term``Doh!'' was added to the Oxford English Dictionary
as an expression of regret.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....10.1
- The state space
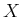 may even
be infinite, but this requires that the set of possible costs is
bounded.
may even
be infinite, but this requires that the set of possible costs is
bounded.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... available.11.1
- Such a problem
could be quite interesting to study, but it will not be considered here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... I-map.11.2
- Ideally, the mapping should
be onto
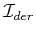 ; however, to facilitate some definitions, this
will not be required.
; however, to facilitate some definitions, this
will not be required.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....11.3
- One notable exception is in the theory of
nondeterministic finite automata, in which it is possible that all
copies of the machine die and there is no possible current state
[891].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... space.11.4
- If you did not read Chapter 4
and are not familiar with manifold concepts, then assume
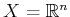 ;
it will not make much difference. Make similar assumptions for
;
it will not make much difference. Make similar assumptions for 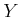 ,
,
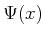 ,
, 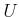 , and
, and
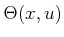 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,11.5
- Assume that all continuous spaces are measure
spaces and all probability density functions are measurable functions
over these spaces.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... functions.11.6
- To appreciate of the size of this space, it can
generally be viewed as an infinite-dimensional vector space (recall
Example 8.5). Consider, for example, representing
each function with a series expansion. To represent any analytic
function exactly over
![$ [0,1]$](img1000.gif) , an infinite sequence of real-valued
coefficients may be needed. Each sequence can be considered as an
infinitely long vector, and the set of all such sequences forms an
infinite-dimensional vector space. See [346,836] for more
background on function spaces and functional
analysis.
, an infinite sequence of real-valued
coefficients may be needed. Each sequence can be considered as an
infinitely long vector, and the set of all such sequences forms an
infinite-dimensional vector space. See [346,836] for more
background on function spaces and functional
analysis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...sec:col-reg.11.7
- This can also be handled, but it just adds
unnecessary complication to the current discussion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... edges.11.8
- This example was significantly refined after
a helpful discussion with Rob Ghrist.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... functions.12.1
- These are single points
that are assigned a nonzero probability mass, which is not allowed,
for example, in the construction of a continuous probability density
function.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sensors:12.2
- This is just one possible sensing
model. Alternative combinations of sensors may be used, provided that
they enable the required motions and decisions to be executed in the
coming motion strategies.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... as12.3
- In practice, a logarithm is applied
to
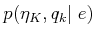 because densities that contain exponentials
usually arise. Taking the logarithm makes the expressions simpler
without affecting the result of the optimization. The
because densities that contain exponentials
usually arise. Taking the logarithm makes the expressions simpler
without affecting the result of the optimization. The 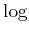 is not
applied here because this level of detail is not covered.
is not
applied here because this level of detail is not covered.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....12.4
- Following
from standard function notation, it is better to use
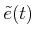 instead of
instead of 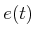 to denote the position at time
to denote the position at time 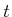 ; however, this
will not be followed.
; however, this
will not be followed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....12.5
- To follow
the notation of Section 11.4 more closely, the motion model
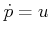 can be used, in which
can be used, in which 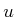 represents the velocity of the
pursuer. Nature actions can be used to model the velocity of the
evader to obtain
represents the velocity of the
pursuer. Nature actions can be used to model the velocity of the
evader to obtain 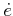 . By integrating
. By integrating 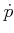 over time,
over time,
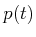 can be obtained for any
can be obtained for any 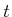 . This means that
. This means that
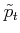 can be
used as a simpler representation of the input history, instead of
directly referring to velocities.
can be
used as a simpler representation of the input history, instead of
directly referring to velocities.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... plan,12.6
- Note that this open-loop plan is
composed of closed-loop motion commands. This is perfectly acceptable
using hierarchical modeling.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
NEXPTIME-hard.12.7
- NEXPTIME is the complexity class of all
problems that can be solved in nondeterministic exponential time.
This is beyond the complexity classes shown in Figure
6.40.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... independent.13.1
- If the coefficients are
placed into an
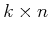 matrix, its rank is
matrix, its rank is 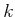 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... speed13.2
- Having a signed speed is somewhat unorthodox.
If the car moves in reverse, then
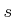 is negative. A more correct
name for
is negative. A more correct
name for 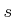 would be velocity in the
would be velocity in the  direction of the body frame,
but this is too cumbersome.
direction of the body frame,
but this is too cumbersome.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....13.3
- In many
works, the speed
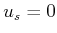 is not included. It appears here so that a
proper termination condition can be defined.
is not included. It appears here so that a
proper termination condition can be defined.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...MurSas93.13.4
- The
original model required a continuous steering angle.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Integrating13.5
- Wherever integrals are performed, it will be
assumed that the integrands are integrable.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
integrators.13.6
- It is called this because in block diagram
representations of systems it is depicted as a chain of integrator
blocks.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... system.13.7
- Be careful not to confuse
control-affine systems with affine control systems, which are of
the form
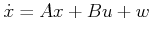 , for some constant matrices
, for some constant matrices 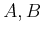 and a
constant vector
and a
constant vector 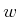 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
resultant13.8
- This is the sum of all forces acting on the point.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... velocity.13.9
- One
important issue to be aware of is that the integral of
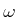 is not
path-invariant (see Example 2.15 of [994]).
is not
path-invariant (see Example 2.15 of [994]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...functional.13.10
- This is the reason why a cost functional has been used throughout the book. It is a function on a
space of functions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....13.11
- Unfortunately,
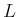 is used here
to represent a cost function, on which a functional
is used here
to represent a cost function, on which a functional 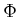 will be
based. This conflicts with using
will be
based. This conflicts with using 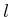 as a cost function and
as a cost function and 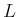 as
the functional in motion planning formulations. This notational
collision remains because
as
the functional in motion planning formulations. This notational
collision remains because 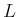 is standard notation for the Lagrangian.
Be careful to avoid confusion.
is standard notation for the Lagrangian.
Be careful to avoid confusion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
action13.12
- The notation
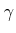 is used instead of
is used instead of 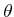 to
avoid conflicting with the car orientation variable
to
avoid conflicting with the car orientation variable 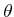 in this
particular example.
in this
particular example.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...symmetry.14.1
- Sometimes in control theory,
the term symmetry applies to Lie groups. This is a different concept
and means that the system is invariant with respect to transformations
in a group such as
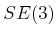 . For example, the dynamics of a car should
not depend on the direction in which the car is pointing.
. For example, the dynamics of a car should
not depend on the direction in which the car is pointing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
spacecraft14.2
- This project was canceled in 2001, but similar
crafts have been under development.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... complicated.14.3
- It may, however,
be possible to compute crude approximations of
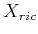 and use them
in planning.
and use them
in planning.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
systems14.4
- The class is all driftless, nilpotent systems. The
term nilpotent will be defined in Section 15.5.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... obstacles.14.5
- One technical point: It is actually only
pseudopolynomial [765] in
 ,
, 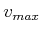 ,
, 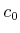 ,
,
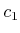 , and the width of the bounding cube in
, and the width of the bounding cube in 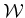 . This means that
the running time is polynomial if the representations of these
parameters are treated as having constant size; however, it is not
polynomial in the actual number of bits needed to truly represent
them.
. This means that
the running time is polynomial if the representations of these
parameters are treated as having constant size; however, it is not
polynomial in the actual number of bits needed to truly represent
them.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
neighborhood15.1
- An open neighborhood of a point
 means an open set that contains
means an open set that contains  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... converges15.2
- This convergence can
be evaluated using the metric
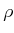 on
on 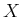 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
analytically.15.3
- It is often surprising to computer scientists
that dynamic programming in this case does not yield an algorithm. It
instead yields a closed-form solution to the problem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... definite15.4
- Nonnegative definite means
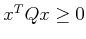 for all
for all
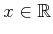 , and positive definite means
, and positive definite means
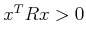 for
all
for
all
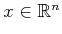 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... principle15.5
- This is often called
Pontryagin's maximum principle, because Pontryagin originally defined
it as a maximization [801]. The Hamiltonian used in
most control literature is negated with respect to Pontryagin's
Hamiltonian; therefore, it becomes minimized. Both names are in
common use.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fig:rsnotation.15.6
- This differs conceptually from the
notation used in [903]. There,
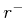 corresponds to
corresponds to 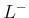 here. The
here. The 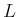 here means that the steering wheel is positioned for a
left turn, but the car is in reverse. This aids in implementing the
rule that
here means that the steering wheel is positioned for a
left turn, but the car is in reverse. This aids in implementing the
rule that 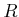 and
and 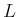 cannot be consecutive in a word.
cannot be consecutive in a word.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
driftless.15.7
- Actually, if the convex hull of
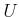 contains an
open set that contains the origin, then a driftless system can be
simulated by rapid switching.
contains an
open set that contains the origin, then a driftless system can be
simulated by rapid switching.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distribution15.8
- This distribution has nothing to do with
probability theory. It is just an unfortunate coincidence of
terminology.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sideways!15.9
- It also moves slightly forward; however, this can
be eliminated by either lengthening the time of the third primitive or
by considering the limit as
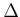 approaches zero.
approaches zero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integrable.15.10
- This system is singular at
the origin. A variant of the Frobenius theorem given here is
technically needed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... algebra15.11
- Intuitively, being an algebra means
that polynomials can be added and multiplied; for all of the required
axioms, see [469].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.