
Next: Homogeneous transformation matrices for Up: 3.3.1 A 2D Kinematic Previous: 3.3.1 A 2D Kinematic
When bodies are attached in a kinematic chain, degrees of freedom are
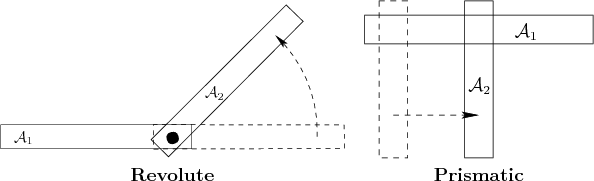
removed. Figure 3.9 shows two different ways in which
a pair of 2D links can be attached. The place at which the links are
attached is called a joint. For a revolute joint, one
link is capable only of rotation with respect to the other. For a
prismatic joint is shown, one link slides along the other. Each
type of joint removes two degrees of freedom from the pair of bodies.
For example, consider a revolute joint that connects
![]() to
to
![]() .
Assume that the point
.
Assume that the point ![]() in the body frame of
in the body frame of
![]() is
permanently fixed to a point
is
permanently fixed to a point ![]() in the body frame of
in the body frame of
![]() .
This implies that the translation of
.
This implies that the translation of
![]() is completely determined
once
is completely determined
once ![]() and
and ![]() are given. Note that
are given. Note that ![]() and
and ![]() depend on
depend on
![]() ,
, ![]() , and
, and ![]() . This implies that
. This implies that
![]() and
and
![]() have a total of four degrees of freedom when attached. The
independent parameters are
have a total of four degrees of freedom when attached. The
independent parameters are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
The task in the remainder of this section is to determine exactly how
the models of
.
The task in the remainder of this section is to determine exactly how
the models of
![]() ,
,
![]() ,
, ![]() ,
,
![]() are transformed when
they are attached in a chain, and to give the expressions in terms of
the independent parameters.
are transformed when
they are attached in a chain, and to give the expressions in terms of
the independent parameters.
 |
Consider the case of a kinematic chain in which each pair of links is
attached by a revolute joint. The first task is to specify the
geometric model for each link,
![]() . Recall that for a single rigid
body, the origin of the body frame determines the axis of rotation.
When defining the model for a link in a kinematic chain, excessive
complications can be avoided by carefully placing the body frame.
Since rotation occurs about a revolute joint, a natural choice
for the origin is the joint between
. Recall that for a single rigid
body, the origin of the body frame determines the axis of rotation.
When defining the model for a link in a kinematic chain, excessive
complications can be avoided by carefully placing the body frame.
Since rotation occurs about a revolute joint, a natural choice
for the origin is the joint between
![]() and
and
![]() for each
for each ![]() . For convenience that will soon become evident, the
. For convenience that will soon become evident, the ![]() -axis
for the body frame of
-axis
for the body frame of
![]() is defined as the line through the two
joints that lie in
is defined as the line through the two
joints that lie in
![]() , as shown in Figure 3.10. For
the last link,
, as shown in Figure 3.10. For
the last link,
![]() , the
, the ![]() -axis can be placed arbitrarily,
assuming that the origin is placed at the joint that connects
-axis can be placed arbitrarily,
assuming that the origin is placed at the joint that connects
![]() to
to
![]() . The body frame for the first link,
. The body frame for the first link,
![]() , can be
placed using the same considerations as for a single rigid body.
, can be
placed using the same considerations as for a single rigid body.
Steven M LaValle 2012-04-20