
Next: What if there are Up: 3.4 Transforming Kinematic Trees Previous: Junctions with more than
Fortunately, it is fine to use different frames when following
different chains; however, one extra piece of information is needed.
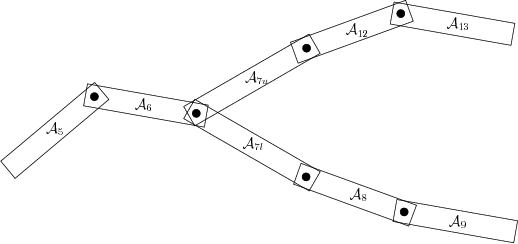
Imagine transforming the whole tree. The variable ![]() will
appear twice, once from each of the upper and lower chains. Let
will
appear twice, once from each of the upper and lower chains. Let
![]() and
and
![]() denote these
denote these ![]() 's. Can
's. Can ![]() really be chosen two different ways? This would imply that the tree
is instead as pictured in Figure 3.24, in which there
are two independently moving links,
really be chosen two different ways? This would imply that the tree
is instead as pictured in Figure 3.24, in which there
are two independently moving links,
![]() and
and
![]() .
.
 |
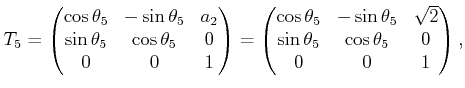 |
(3.73) |
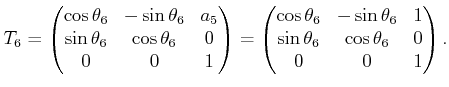 |
(3.74) |
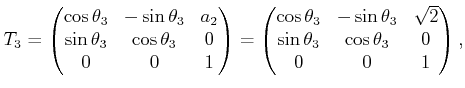 |
(3.76) |
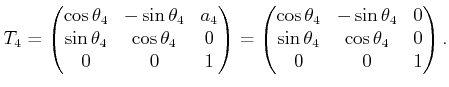 |
(3.77) |
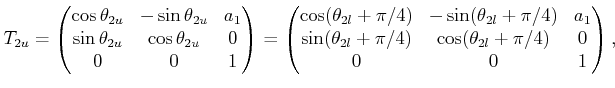 |
(3.78) |
For a 3D tree of bodies the same general principles may be followed. In some cases, there will not be any complications that involve special considerations of junctions and constraints. One example of this is the transformation of flexible molecules because all consecutive rotation axes intersect, and junctions occur directly at these points of intersection. In general, however, the DH parameter technique may be applied for each chain, and then the appropriate constraints have to be determined and applied to represent the true degrees of freedom of the tree. The Khalil-Kleinfinger parameterization conveniently captures the resulting solution [524].
Steven M LaValle 2012-04-20