
Next: ``Wreckless'' driving Up: 1.2 Motivational Examples and Previous: Virtual humans and humanoid
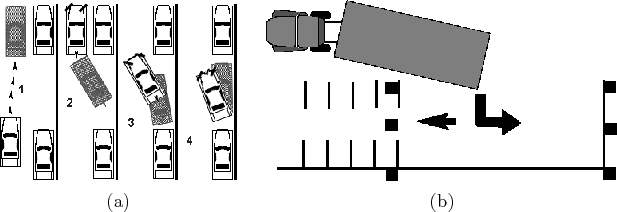 |
The planning problems discussed so far have not involved differential constraints, which are the main focus in Part IV. Consider the problem of parking slow-moving vehicles, as shown in Figure 1.11. Most people have a little difficulty with parallel parking a car and much greater difficulty parking a truck with a trailer. Imagine the difficulty of parallel parking an airport baggage train! See Chapter 13 for many related examples. What makes these problems so challenging? A car is constrained to move in the direction that the rear wheels are pointing. Maneuvering the car around obstacles therefore becomes challenging. If all four wheels could turn to any orientation, this problem would vanish. The term nonholonomic planning encompasses parking problems and many others. Figure 1.12a shows a humorous driving problem. Figure 1.12b shows an extremely complicated vehicle for which nonholonomic planning algorithms were developed and applied in industry.
Steven M LaValle 2012-04-20