
Next: Using quaternion multiplication Up: 4.2.2 3D Rigid Bodies: Previous: Using complex numbers to
The manner in which complex numbers were used to represent 2D
rotations will now be adapted to using quaternions to represent 3D
rotations. Let
![]() represent the set of quaternions, in which
each quaternion,
represent the set of quaternions, in which
each quaternion,
![]() , is represented as
, is represented as
![]() , and
, and
![]() . A quaternion can be considered as a
four-dimensional vector. The symbols
. A quaternion can be considered as a
four-dimensional vector. The symbols ![]() ,
, ![]() , and
, and ![]() are used to
denote three ``imaginary'' components of the quaternion. The
following relationships are defined:
are used to
denote three ``imaginary'' components of the quaternion. The
following relationships are defined:
![]() ,
from which it follows that
,
from which it follows that ![]() ,
, ![]() , and
, and ![]() . Using
these, multiplication of two quaternions,
. Using
these, multiplication of two quaternions,
![]() and
and
![]() , can be derived to
obtain
, can be derived to
obtain
![]() , in which
, in which
For convenience, quaternion multiplication can be expressed in terms
of vector multiplications, a dot product, and a cross product. Let
![]() be a three-dimensional vector that represents the
final three quaternion components. The first component of
be a three-dimensional vector that represents the
final three quaternion components. The first component of
![]() is
is
![]() . The final three components are
given by the three-dimensional vector
. The final three components are
given by the three-dimensional vector
![]() .
.
In the same way that unit complex numbers were needed for ![]() , unit
quaternions are needed for
, unit
quaternions are needed for ![]() , which means that
, which means that
![]() is
restricted to quaternions for which
is
restricted to quaternions for which
![]() . Note
that this forms a subgroup because the multiplication of unit
quaternions yields a unit quaternion, and the other group axioms hold.
. Note
that this forms a subgroup because the multiplication of unit
quaternions yields a unit quaternion, and the other group axioms hold.
 |
The next step is to describe a mapping from unit quaternions to
![]() . Let the unit quaternion
. Let the unit quaternion
![]() map to the
matrix
map to the
matrix
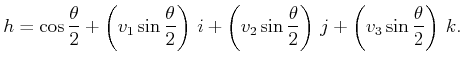 |
(4.21) |
Unfortunately, this representation is not unique. It can be verified
in (4.20) that
![]() . A nice geometric
interpretation is given in Figure 4.10. The quaternions
. A nice geometric
interpretation is given in Figure 4.10. The quaternions
![]() and
and ![]() represent the same rotation because a rotation of
represent the same rotation because a rotation of
![]() about the direction
about the direction ![]() is equivalent to a rotation of
is equivalent to a rotation of
![]() about the direction
about the direction ![]() . Consider the quaternion
representation of the second expression of rotation with respect to
the first. The real part is
. Consider the quaternion
representation of the second expression of rotation with respect to
the first. The real part is
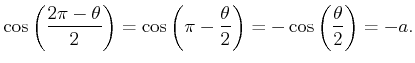 |
(4.22) |
![$\displaystyle - v \sin\left(\frac{2 \pi - \theta}{2}\right) = - v \sin\left(\pi...
...eta}{2}\right) = - v \sin\left(\frac{\theta}{2}\right) = [ -b \;\; -c \;\; -d].$](img1295.gif) |
(4.23) |
This can be fixed by the identification trick. Note that the set of
unit quaternions is homeomorphic to
![]() because of the constraint
because of the constraint
![]() . The algebraic properties of quaternions
are not relevant at this point. Just imagine each
. The algebraic properties of quaternions
are not relevant at this point. Just imagine each ![]() as an element
of
as an element
of
![]() , and the constraint
, and the constraint
![]() forces the
points to lie on
forces the
points to lie on
![]() . Using identification, declare
. Using identification, declare ![]() for all unit quaternions. This means that the antipodal points of
for all unit quaternions. This means that the antipodal points of
![]() are identified. Recall from the end of Section
4.1.2 that when antipodal points are identified,
are identified. Recall from the end of Section
4.1.2 that when antipodal points are identified,
![]() . Hence,
. Hence,
![]() , which can be
considered as the set of all lines through the origin of
, which can be
considered as the set of all lines through the origin of
![]() , but
this is hard to visualize. The representation of
, but
this is hard to visualize. The representation of
![]() in Figure
4.5 can be extended to
in Figure
4.5 can be extended to
![]() . Start with
. Start with
![]() , and make three different kinds of identifications, one
for each pair of opposite cube faces, and add all of the points to the
manifold. For each kind of identification a twist needs to be made
(without the twist,
, and make three different kinds of identifications, one
for each pair of opposite cube faces, and add all of the points to the
manifold. For each kind of identification a twist needs to be made
(without the twist,
![]() would be obtained). For example, in the
would be obtained). For example, in the
![]() direction, let
direction, let
![]() for all
for all
![]() .
.
One way to force uniqueness of rotations is to require staying in the
``upper half'' of
![]() . For example, require that
. For example, require that ![]() , as
long as the boundary case of
, as
long as the boundary case of ![]() is handled properly because of
antipodal points at the equator of
is handled properly because of
antipodal points at the equator of
![]() . If
. If ![]() , then require
that
, then require
that ![]() . However, if
. However, if ![]() , then require that
, then require that ![]() because points such as
because points such as
![]() and
and ![]() are the same
rotation. Finally, if
are the same
rotation. Finally, if ![]() , then only
, then only ![]() is allowed. If such
restrictions are made, it is important, however, to remember the
connectivity of
is allowed. If such
restrictions are made, it is important, however, to remember the
connectivity of
![]() . If a path travels across the equator of
. If a path travels across the equator of
![]() , it must be mapped to the appropriate place in the ``northern
hemisphere.'' At the instant it hits the equator, it must move to the
antipodal point. These concepts are much easier to visualize if you
remove a dimension and imagine them for
, it must be mapped to the appropriate place in the ``northern
hemisphere.'' At the instant it hits the equator, it must move to the
antipodal point. These concepts are much easier to visualize if you
remove a dimension and imagine them for
![]() , as
described at the end of Section 4.1.2.
, as
described at the end of Section 4.1.2.
Steven M LaValle 2012-04-20