The most interesting and complicated situations occur when there is a
continuum of solutions. For example, if one of the constraints is
removed, then a one-dimensional set of solutions can be obtained.
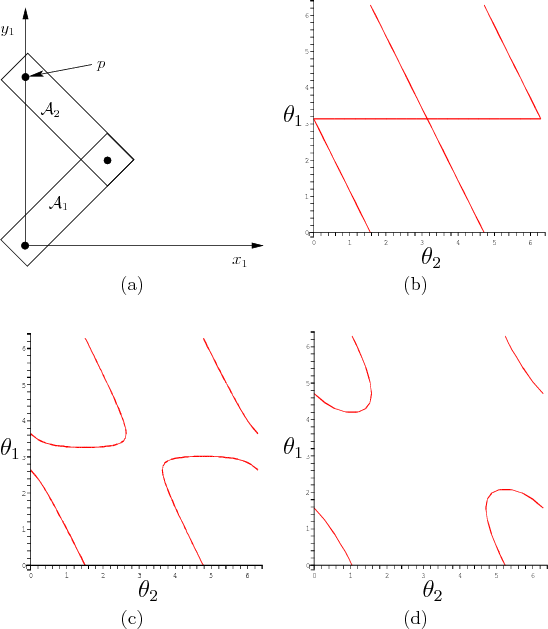
Suppose only one variable is constrained for the example in Figure
4.22. Intuitively, this should yield a one-dimensional
variety. Set the 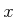 coordinate to 0, which yields
coordinate to 0, which yields
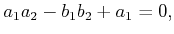 |
(4.65) |
and allow any possible value for 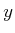 . As shown in Figure
4.23a, the point
. As shown in Figure
4.23a, the point 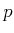 must follow the
must follow the 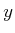 -axis. (This is
equivalent to a three-bar linkage that can be constructed by making a
third joint that is prismatic and forced to stay along the
-axis. (This is
equivalent to a three-bar linkage that can be constructed by making a
third joint that is prismatic and forced to stay along the 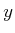 -axis.)
Figure 4.23b shows the resulting variety
-axis.)
Figure 4.23b shows the resulting variety
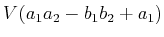 but plotted in
but plotted in
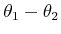 coordinates to
reduce the dimension from
coordinates to
reduce the dimension from 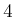 to
to 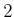 for visualization purposes. To
correctly interpret the figures in Figure 4.23, recall
that the topology is
for visualization purposes. To
correctly interpret the figures in Figure 4.23, recall
that the topology is
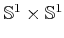 , which means that the top and
bottom are identified, and also the sides are identified. The center
of Figure 4.23b, which corresponds to
, which means that the top and
bottom are identified, and also the sides are identified. The center
of Figure 4.23b, which corresponds to
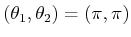 , prevents the variety from being a
manifold. The resulting space is actually homeomorphic to two circles
that touch at a point. Thus, even with such a simple example, the
nice manifold structure may disappear. Observe that at
, prevents the variety from being a
manifold. The resulting space is actually homeomorphic to two circles
that touch at a point. Thus, even with such a simple example, the
nice manifold structure may disappear. Observe that at 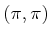 the links are completely overlapped, and the point
the links are completely overlapped, and the point 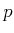 of
of
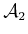 is
placed at
is
placed at 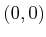 in
in 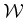 . The horizontal line in Figure
4.23b corresponds to keeping the two links overlapping
and swinging them around together by varying
. The horizontal line in Figure
4.23b corresponds to keeping the two links overlapping
and swinging them around together by varying 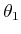 . The diagonal
lines correspond to moving along configurations such as the one shown
in Figure 4.23a. Note that the links and the
. The diagonal
lines correspond to moving along configurations such as the one shown
in Figure 4.23a. Note that the links and the 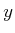 -axis
always form an isosceles triangle, which can be used to show that the
solution set is any pair of angles,
-axis
always form an isosceles triangle, which can be used to show that the
solution set is any pair of angles, 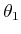 ,
, 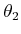 for which
for which
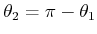 . This is the reason why the diagonal
curves in Figure 4.23b are linear. Figures
4.23c and 4.23d show the varieties for the
constraints
. This is the reason why the diagonal
curves in Figure 4.23b are linear. Figures
4.23c and 4.23d show the varieties for the
constraints
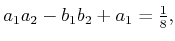 |
(4.66) |
and
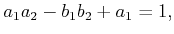 |
(4.67) |
respectively. In these cases, the point 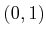 in
in
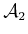 must follow
the
must follow
the 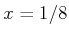 and
and 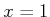 axes, respectively. The varieties are
manifolds, which are homeomorphic to
axes, respectively. The varieties are
manifolds, which are homeomorphic to
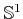 . The sequence from Figure
4.23b to 4.23d can be imagined as part
of an animation in which the variety shrinks into a small circle.
Eventually, it shrinks to a point for the case
. The sequence from Figure
4.23b to 4.23d can be imagined as part
of an animation in which the variety shrinks into a small circle.
Eventually, it shrinks to a point for the case
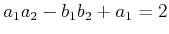 , because the only solution is when
, because the only solution is when
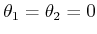 .
Beyond this, the variety is the empty set because there are no
solutions. Thus, by allowing one constraint to vary, four different
topologies are obtained: 1) two circles joined at a point, 2) a
circle, 3) a point, and 4) the empty set.
.
Beyond this, the variety is the empty set because there are no
solutions. Thus, by allowing one constraint to vary, four different
topologies are obtained: 1) two circles joined at a point, 2) a
circle, 3) a point, and 4) the empty set.
Figure 4.23:
A single constraint was added to the
point  on
on
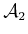 , as shown in (a). The curves in (b), (c), and (d)
depict the variety for the cases of
, as shown in (a). The curves in (b), (c), and (d)
depict the variety for the cases of 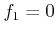 ,
, 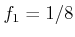 , and
, and 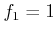 ,
respectively.
,
respectively.
 |
Steven M LaValle
2012-04-20

![]() coordinate to 0, which yields
coordinate to 0, which yields
