
Next: 4.4.3 Defining the Variety Up: 4.4.2 Kinematic Chains in Previous: A one-dimensional variety
Since visualization is still possible with one more dimension, suppose
there are three links,
![]() ,
,
![]() , and
, and
![]() . The C-space can be
visualized as a 3D cube with opposite faces identified. Each
coordinate
. The C-space can be
visualized as a 3D cube with opposite faces identified. Each
coordinate ![]() ranges from 0 to
ranges from 0 to ![]() , for which
, for which
![]() . Suppose that each link has length
. Suppose that each link has length ![]() to obtain
to obtain
![]() . A point
. A point
![]() is transformed as
is transformed as
To obtain polynomials, let
![]() and
and
![]() , which results in
, which results in
Again, consider imposing a single constraint,
Increasing the required ![]() value for the constraint on the final
point causes the variety to shrink. Snapshots for
value for the constraint on the final
point causes the variety to shrink. Snapshots for ![]() and
and
![]() are shown in Figure 4.25. At
are shown in Figure 4.25. At ![]() , the
variety is not a manifold, but it then changes to
, the
variety is not a manifold, but it then changes to
![]() . Eventually,
this sphere is reduced to a point at
. Eventually,
this sphere is reduced to a point at ![]() , and then for
, and then for ![]() the variety is empty.
the variety is empty.
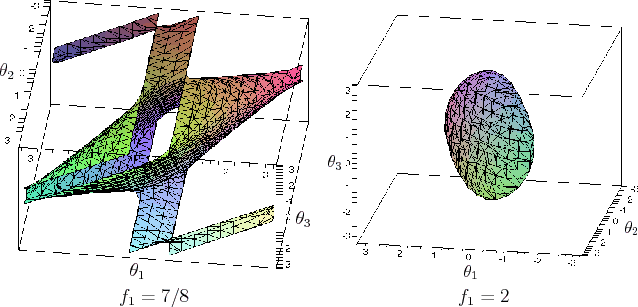 |
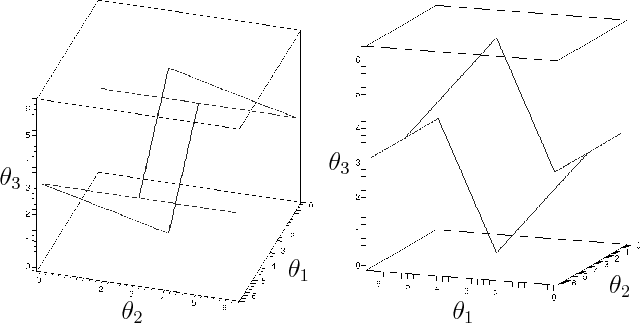 |
Instead of the constraint ![]() , we could instead constrain the
, we could instead constrain the
![]() coordinate of
coordinate of ![]() to obtain
to obtain ![]() . This yields another 2D
variety. If both constraints are enforced simultaneously, then the
result is the intersection of the two original varieties. For
example, suppose
. This yields another 2D
variety. If both constraints are enforced simultaneously, then the
result is the intersection of the two original varieties. For
example, suppose ![]() and
and ![]() . This is equivalent to a
kind of four-bar mechanism [310], in which the
fourth link,
. This is equivalent to a
kind of four-bar mechanism [310], in which the
fourth link,
![]() , is fixed along the
, is fixed along the ![]() -axis from 0 to
-axis from 0 to ![]() . The
resulting variety,
. The
resulting variety,
Steven M LaValle 2012-04-20