
Next: 5.2.3 Low-Dispersion Sampling Up: 5.2.2 Random Sampling Previous: Pseudorandom number generation
Thus, it is important to realize that even the ``random'' samples are
deterministic. They are designed to optimize performance on
statistical tests. Many sophisticated statistical tests of uniform
randomness are used. One of the simplest, the chi-square test,
is described here. This test measures how far computed statistics are
from their expected value. As a simple example, suppose
![]() and is partitioned into a
and is partitioned into a ![]() by
by ![]() array of
array of ![]() square
boxes. If a set
square
boxes. If a set ![]() of
of ![]() samples is chosen at random, then
intuitively each box should receive roughly
samples is chosen at random, then
intuitively each box should receive roughly ![]() of the samples.
An error function can be defined to measure how far from true this
intuition is:
of the samples.
An error function can be defined to measure how far from true this
intuition is:
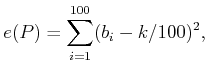 |
(5.18) |
 |
This irregularity can be observed in terms of Voronoi
diagrams, as shown in Figure
5.3. The Voronoi diagram partitions
![]() into
regions based on the samples. Each sample
into
regions based on the samples. Each sample ![]() has an associated
Voronoi region
has an associated
Voronoi region
![]() . For any point
. For any point
![]() ,
, ![]() is
the closest sample to
is
the closest sample to ![]() using Euclidean distance. The different
sizes and shapes of these regions give some indication of the
required irregularity of random sampling. This irregularity may be
undesirable for sampling-based motion planning and is somewhat
repaired by the deterministic sampling methods of Sections
5.2.3 and 5.2.4 (however, these methods also
have drawbacks).
using Euclidean distance. The different
sizes and shapes of these regions give some indication of the
required irregularity of random sampling. This irregularity may be
undesirable for sampling-based motion planning and is somewhat
repaired by the deterministic sampling methods of Sections
5.2.3 and 5.2.4 (however, these methods also
have drawbacks).
Steven M LaValle 2012-04-20