
Next: Infinite grid sequences Up: 5.2.3 Low-Dispersion Sampling Previous: Dispersion definition
Optimizing dispersion forces the points to be distributed more
uniformly over ![]() . This causes them to fail statistical tests, but
the point distribution is often better for motion planning purposes.
Consider the best way to reduce dispersion if
. This causes them to fail statistical tests, but
the point distribution is often better for motion planning purposes.
Consider the best way to reduce dispersion if ![]() is the
is the ![]() metric and
metric and
![]() . Suppose that the number of samples,
. Suppose that the number of samples, ![]() , is
given. Optimal dispersion is obtained by partitioning
, is
given. Optimal dispersion is obtained by partitioning ![]() into a
grid of cubes and placing a point at the center of each cube, as
shown for
into a
grid of cubes and placing a point at the center of each cube, as
shown for ![]() and
and ![]() in Figure 5.5a. The
number of cubes per axis must be
in Figure 5.5a. The
number of cubes per axis must be
![]() , in
which
, in
which
![]() denotes the floor. If
denotes the floor. If
![]() is not an integer, then there are leftover points that
may be placed anywhere without affecting the dispersion. Notice that
is not an integer, then there are leftover points that
may be placed anywhere without affecting the dispersion. Notice that
![]() just gives the number of points per axis for a grid of
just gives the number of points per axis for a grid of
![]() points in
points in ![]() dimensions. The resulting grid will be referred to
as a Sukharev grid [922].
dimensions. The resulting grid will be referred to
as a Sukharev grid [922].
The dispersion obtained by the Sukharev grid is the best possible.
Therefore, a useful lower bound can be given for any set ![]() of
of
![]() samples [922]:
samples [922]:
At this point you might wonder why ![]() was used instead of
was used instead of
![]() , which seems more natural. This is because the
, which seems more natural. This is because the ![]() case is
extremely difficult to optimize (except in
case is
extremely difficult to optimize (except in
![]() , where a tiling of
equilateral triangles can be made, with a point in the center of each
one). Even the simple problem of determining the best way to
distribute a fixed number of points in
, where a tiling of
equilateral triangles can be made, with a point in the center of each
one). Even the simple problem of determining the best way to
distribute a fixed number of points in ![]() is unsolved for most
values of
is unsolved for most
values of ![]() . See [241] for extensive treatment of this
problem.
. See [241] for extensive treatment of this
problem.
Suppose now that other topologies are considered instead of
![]() . Let
. Let
![]() , in which the identification produces
a torus. The situation is quite different because
, in which the identification produces
a torus. The situation is quite different because ![]() no longer has a
boundary. The Sukharev grid still produces optimal dispersion, but it
can also be shifted without increasing the dispersion. In this case,
a standard grid may also be used, which has the same number of
points as the Sukharev grid but is translated to the origin. Thus,
the first grid point is
no longer has a
boundary. The Sukharev grid still produces optimal dispersion, but it
can also be shifted without increasing the dispersion. In this case,
a standard grid may also be used, which has the same number of
points as the Sukharev grid but is translated to the origin. Thus,
the first grid point is ![]() , which is actually the same as
, which is actually the same as ![]() other points by identification. If
other points by identification. If ![]() represents a cylinder and the
number of points,
represents a cylinder and the
number of points, ![]() , is given, then it is best to just use the
Sukharev grid. It is possible, however, to shift each coordinate that
behaves like
, is given, then it is best to just use the
Sukharev grid. It is possible, however, to shift each coordinate that
behaves like
![]() . If
. If ![]() is rectangular but not a square, a good
grid can still be made by tiling the space with cubes. In some cases
this will produce optimal dispersion. For complicated spaces such as
is rectangular but not a square, a good
grid can still be made by tiling the space with cubes. In some cases
this will produce optimal dispersion. For complicated spaces such as
![]() , no grid exists in the sense defined so far. It is possible,
however, to generate grids on the faces of an inscribed Platonic solid
[251] and lift the samples to
, no grid exists in the sense defined so far. It is possible,
however, to generate grids on the faces of an inscribed Platonic solid
[251] and lift the samples to
![]() with relatively little
distortion [987]. For example, to sample
with relatively little
distortion [987]. For example, to sample
![]() , Sukharev
grids can be placed on each face of a cube. These are lifted to
obtain the warped grid shown in Figure 5.6a.
, Sukharev
grids can be placed on each face of a cube. These are lifted to
obtain the warped grid shown in Figure 5.6a.
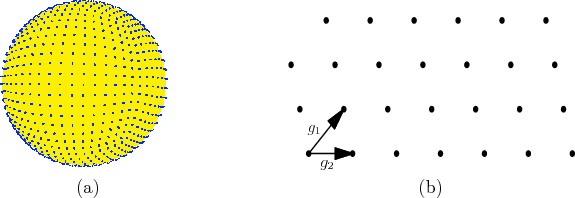 |
One nice property of grids is that they have a lattice structure.
This means that neighboring points can be obtained very easily be
adding or subtracting vectors. Let ![]() be an
be an ![]() -dimensional vector
called a generator. A point on a
lattice can be expressed as
-dimensional vector
called a generator. A point on a
lattice can be expressed as
Steven M LaValle 2012-04-20