Once again, let
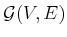 represent a topological graph in which
represent a topological graph in which 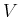 is
a set of vertices and
is
a set of vertices and 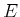 is the set of paths that map into
is the set of paths that map into
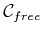 .
Under the multiple-query philosophy, motion planning is divided into
two phases of computation:
.
Under the multiple-query philosophy, motion planning is divided into
two phases of computation:
- [] Preprocessing Phase: During the preprocessing phase,
substantial effort is invested to build
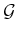 in a way that is useful
for quickly answering future queries. For this reason, it is called a
roadmap, which in some sense should be accessible from every part
of
in a way that is useful
for quickly answering future queries. For this reason, it is called a
roadmap, which in some sense should be accessible from every part
of
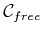 .
.
- [] Query Phase: During the query phase, a pair,
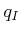 and
and 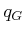 , is given. Each configuration must be connected easily
to
, is given. Each configuration must be connected easily
to 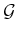 using a local planner. Following this, a discrete search is
performed using any of the algorithms in Section 2.2 to
obtain a sequence of edges that forms a path from
using a local planner. Following this, a discrete search is
performed using any of the algorithms in Section 2.2 to
obtain a sequence of edges that forms a path from 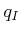 to
to
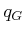 .
.
Figure 5.25:
The basic construction algorithm for
sampling-based roadmaps. Note that 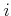 is not incremented if
is not incremented if
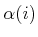 is in collision. This forces
is in collision. This forces 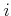 to correctly count the
number of vertices in the roadmap.
to correctly count the
number of vertices in the roadmap.
 |
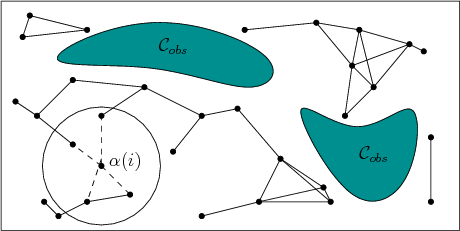
Figure 5.26:
The sampling-based roadmap is
constructed incrementally by attempting to connect each new sample,
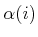 , to nearby vertices in the roadmap.
, to nearby vertices in the roadmap.
 |
Subsections
Steven M LaValle
2012-04-20

![]() represent a topological graph in which
represent a topological graph in which ![]() is
a set of vertices and
is
a set of vertices and ![]() is the set of paths that map into
is the set of paths that map into
![]() .
Under the multiple-query philosophy, motion planning is divided into
two phases of computation:
.
Under the multiple-query philosophy, motion planning is divided into
two phases of computation:

