
Next: Further Reading Up: 5.6.3 Heuristics for Improving Previous: Bridge-test sampling [465]
 |
Rather than trying to sample close to the boundary, another strategy
is to force the samples to be as far from the boundary as possible.
Let ![]() be a metric space. Let a maximal ball be a ball
be a metric space. Let a maximal ball be a ball
![]() such that no other ball can be a proper subset.
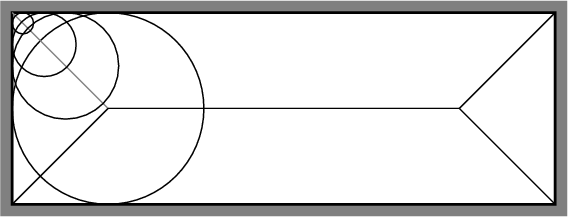
The centers of all maximal balls trace out a one-dimensional set of
points referred to as the medial axis. A simple example of a
medial axis is shown for a rectangular subset of
such that no other ball can be a proper subset.
The centers of all maximal balls trace out a one-dimensional set of
points referred to as the medial axis. A simple example of a
medial axis is shown for a rectangular subset of
![]() in Figure
5.30. The medial axis in
in Figure
5.30. The medial axis in
![]() is based on the largest
balls that can be inscribed in
is based on the largest
balls that can be inscribed in
![]() . Sampling on the
medial axis is generally difficult, especially because the
representation of
. Sampling on the
medial axis is generally difficult, especially because the
representation of
![]() is implicit. Distance information from
collision checking can be used to start with a sample,
is implicit. Distance information from
collision checking can be used to start with a sample,
![]() ,
and iteratively perturb it to increase its distance from
,
and iteratively perturb it to increase its distance from
![]() [635,971]. Sampling on the
medial axis of
[635,971]. Sampling on the
medial axis of
![]() has also been proposed
[455]. In this case, the medial axis in
has also been proposed
[455]. In this case, the medial axis in
![]() is easier to compute, and it can be used to heuristically guide the
placement of good roadmap vertices in
is easier to compute, and it can be used to heuristically guide the
placement of good roadmap vertices in
![]() .
.
Steven M LaValle 2012-04-20