
Next: General position issues Up: 6.2.2 Vertical Cell Decomposition Previous: 6.2.2 Vertical Cell Decomposition
We next present an algorithm that constructs a vertical cell
decomposition [189], which partitions
![]() into a finite
collection of 2-cells and 1-cells. Each 2-cell is either a trapezoid
that has vertical sides or a triangle (which is a degenerate
trapezoid). For this reason, the method is sometimes called trapezoidal decomposition. The decomposition is defined as follows.
Let
into a finite
collection of 2-cells and 1-cells. Each 2-cell is either a trapezoid
that has vertical sides or a triangle (which is a degenerate
trapezoid). For this reason, the method is sometimes called trapezoidal decomposition. The decomposition is defined as follows.
Let ![]() denote the set of vertices used to define
denote the set of vertices used to define
![]() . At every
. At every
![]() , try to extend rays upward and downward through
, try to extend rays upward and downward through
![]() ,
until
,
until
![]() is hit. There are four possible cases, as shown in
Figure 6.2, depending on whether or not it is possible
to extend in each of the two directions. If
is hit. There are four possible cases, as shown in
Figure 6.2, depending on whether or not it is possible
to extend in each of the two directions. If
![]() is partitioned
according to these rays, then a vertical decomposition results.
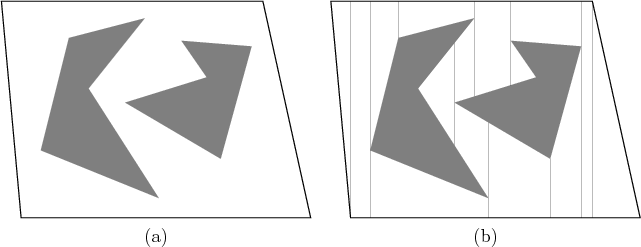
Extending these rays for the example in Figure 6.3a
leads to the decomposition of
is partitioned
according to these rays, then a vertical decomposition results.
Extending these rays for the example in Figure 6.3a
leads to the decomposition of
![]() shown in Figure
6.3b. Note that only trapezoids and triangles are
obtained for the 2-cells in
shown in Figure
6.3b. Note that only trapezoids and triangles are
obtained for the 2-cells in
![]() .
.
 |
Every 1-cell is a vertical segment that serves as the border between
two 2-cells. We must ensure that the topology of
![]() is
correctly represented. Recall that
is
correctly represented. Recall that
![]() was defined to be an open
set. Every 2-cell is actually defined to be an open set in
was defined to be an open
set. Every 2-cell is actually defined to be an open set in
![]() ;
thus, it is the interior of a trapezoid or triangle. The 1-cells are
the interiors of segments. It is tempting to make 0-cells, which
correspond to the endpoints of segments, but these are not allowed
because they lie in
;
thus, it is the interior of a trapezoid or triangle. The 1-cells are
the interiors of segments. It is tempting to make 0-cells, which
correspond to the endpoints of segments, but these are not allowed
because they lie in
![]() .
.
Steven M LaValle 2012-04-20