
Next: 1.4.2 Planners Up: 1.4 Algorithms, Planners, and Previous: 1.4 Algorithms, Planners, and
What is a planning algorithm? This is a difficult question, and a precise mathematical definition will not be given in this book. Instead, the general idea will be explained, along with many examples of planning algorithms. A more basic question is, What is an algorithm? One answer is the classical Turing machine model, which is used to define an algorithm in theoretical computer science. A Turing machine is a finite state machine with a special head that can read and write along an infinite piece of tape, as depicted in Figure 1.15. The Church-Turing thesis states that an algorithm is a Turing machine (see [462,891] for more details). The input to the algorithm is encoded as a string of symbols (usually a binary string) and then is written to the tape. The Turing machine reads the string, performs computations, and then decides whether to accept or reject the string. This version of the Turing machine only solves decision problems; however, there are straightforward extensions that can yield other desired outputs, such as a plan.
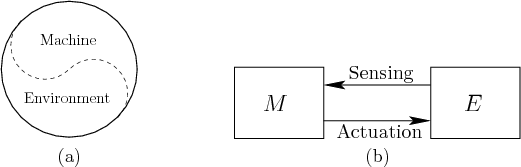 |
The Turing model is reasonable for many of the algorithms in this book; however, others may not exactly fit. The trouble with using the Turing machine in some situations is that plans often interact with the physical world. As indicated in Figure 1.16, the boundary between the machine and the environment is an arbitrary line that varies from problem to problem. Once drawn, sensors provide information about the environment; this provides input to the machine during execution. The machine then executes actions, which provides actuation to the environment. The actuation may alter the environment in some way that is later measured by sensors. Therefore, the machine and its environment are closely coupled during execution. This is fundamental to robotics and many other fields in which planning is used.
Using the Turing machine as a foundation for algorithms usually implies that the physical world must be first carefully modeled and written on the tape before the algorithm can make decisions. If changes occur in the world during execution of the algorithm, then it is not clear what should happen. For example, a mobile robot could be moving in a cluttered environment in which people are walking around. As another example, a robot might throw an object onto a table without being able to precisely predict how the object will come to rest. It can take measurements of the results with sensors, but it again becomes a difficult task to determine how much information should be explicitly modeled and written on the tape. The on-line algorithm model is more appropriate for these kinds of problems [510,768,892]; however, it still does not capture a notion of algorithms that is broad enough for all of the topics of this book.
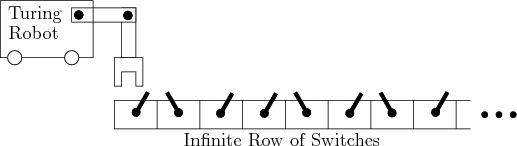 |
Processes that occur in a physical world are more complicated than the interaction between a state machine and a piece of tape filled with symbols. It is even possible to simulate the tape by imagining a robot that interacts with a long row of switches as depicted in Figure 1.17. The switches serve the same purpose as the tape, and the robot carries a computer that can simulate the finite state machine.1.1The complicated interaction allowed between a robot and its environment could give rise to many other models of computation.1.2 Thus, the term algorithm will be used somewhat less formally than in the theory of computation. Both planners and plans are considered as algorithms in this book.
Steven M LaValle 2012-04-20