Recall the logical predicates that were formed in Section
3.1. They will be used again here, but now they are defined
with a little more flexibility. For any
![$ f \in {\mathbb{Q}}[x_1,\ldots, x_n]$](img2245.gif) ,
an atom is an expression of the form
,
an atom is an expression of the form
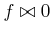 , in which
, in which
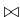 may be any relation in the set
may be any relation in the set
 . In Section 3.1, such expressions were used to
define logical predicates. Here, we assume that relations other than
. In Section 3.1, such expressions were used to
define logical predicates. Here, we assume that relations other than
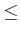 can be used and that the vector of polynomial variables lies
in
can be used and that the vector of polynomial variables lies
in
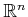 .
.
A quantifier-free formula,
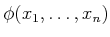 , is a logical
predicate composed of atoms and logical connectives, ``and,'' ``or,''
and ``not,'' which are denoted by
, is a logical
predicate composed of atoms and logical connectives, ``and,'' ``or,''
and ``not,'' which are denoted by 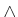 ,
, 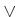 , and
, and 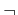 ,
respectively. Each atom itself is considered as a logical predicate
that yields TRUE if and only if the relation is satisfied when the
polynomial is evaluated at the point
,
respectively. Each atom itself is considered as a logical predicate
that yields TRUE if and only if the relation is satisfied when the
polynomial is evaluated at the point
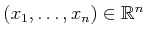 .
.
Example 6..2 (An Example Predicate)
Let
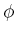
be a predicate over
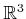
, defined as
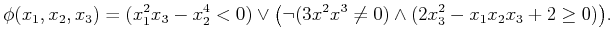 |
(6.8) |
The precedence order of the connectives follows the laws of Boolean
algebra.

Let a quantifier 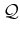 be either of the symbols,
be either of the symbols, 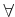 ,
which means ``for all,'' or
,
which means ``for all,'' or 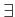 , which means ``there exists.''
A Tarski sentence
, which means ``there exists.''
A Tarski sentence 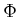 is a logical predicate that may
additionally involve quantifiers on some or all of the variables. In
general, a Tarski sentence takes the form
is a logical predicate that may
additionally involve quantifiers on some or all of the variables. In
general, a Tarski sentence takes the form
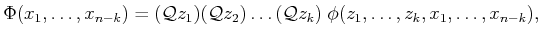 |
(6.9) |
in which the 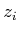 are the quantified variables, the
are the quantified variables, the 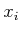 are
the free variables, and
are
the free variables, and 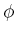 is a quantifier-free formula.
The quantifiers do not necessarily have to appear at the left to be a
valid Tarski sentence; however, any expression can be manipulated into
an equivalent expression that has all quantifiers in front, as shown
in (6.9). The procedure for moving quantifiers to the
front is as follows [705]: 1) Eliminate any redundant
quantifiers; 2) rename some of the variables to ensure that the same
variable does not appear both free and bound; 3) move negation symbols
as far inward as possible; and 4) push the quantifiers to the left.
is a quantifier-free formula.
The quantifiers do not necessarily have to appear at the left to be a
valid Tarski sentence; however, any expression can be manipulated into
an equivalent expression that has all quantifiers in front, as shown
in (6.9). The procedure for moving quantifiers to the
front is as follows [705]: 1) Eliminate any redundant
quantifiers; 2) rename some of the variables to ensure that the same
variable does not appear both free and bound; 3) move negation symbols
as far inward as possible; and 4) push the quantifiers to the left.
Example 6..3 (Several Tarski Sentences)
Tarski sentences that have no free variables are either
TRUE or
FALSE in general because there are no arguments on which the results
depend. The sentence
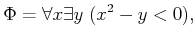 |
(6.10) |
is
TRUE because for any
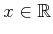
, some
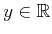
can always be
chosen so that
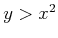
. In the general notation of
(
6.9), this example becomes
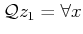
,
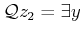
, and
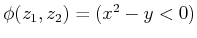
.
Swapping the order of the quantifiers yields the Tarski sentence
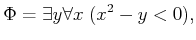 |
(6.11) |
which is
FALSE because for any
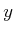
, there is always an

such that
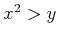
.
Now consider a Tarski sentence that has a free variable:
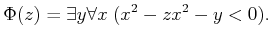 |
(6.12) |
This yields a function
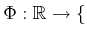 TRUE
TRUE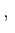 FALSE
FALSE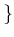
, in
which
 |
(6.13) |
An equivalent quantifier-free formula
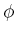
can be defined as
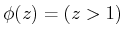
, which takes on the same truth values as the
Tarski sentence in (
6.12). This might make you wonder
whether it is always possible to make a simplification that eliminates
the quantifiers. This is called the
quantifier-elimination
problem, which will be explained shortly.

Steven M LaValle
2012-04-20

![]() ,
an atom is an expression of the form
,
an atom is an expression of the form
![]() , in which
, in which
![]() may be any relation in the set
may be any relation in the set
![]() . In Section 3.1, such expressions were used to
define logical predicates. Here, we assume that relations other than
. In Section 3.1, such expressions were used to
define logical predicates. Here, we assume that relations other than
![]() can be used and that the vector of polynomial variables lies
in
can be used and that the vector of polynomial variables lies
in
![]() .
.
![]() , is a logical
predicate composed of atoms and logical connectives, ``and,'' ``or,''
and ``not,'' which are denoted by
, is a logical
predicate composed of atoms and logical connectives, ``and,'' ``or,''
and ``not,'' which are denoted by ![]() ,
, ![]() , and
, and ![]() ,
respectively. Each atom itself is considered as a logical predicate
that yields TRUE if and only if the relation is satisfied when the
polynomial is evaluated at the point
,
respectively. Each atom itself is considered as a logical predicate
that yields TRUE if and only if the relation is satisfied when the
polynomial is evaluated at the point
![]() .
.
![]() be either of the symbols,
be either of the symbols, ![]() ,
which means ``for all,'' or
,
which means ``for all,'' or ![]() , which means ``there exists.''
A Tarski sentence
, which means ``there exists.''
A Tarski sentence ![]() is a logical predicate that may
additionally involve quantifiers on some or all of the variables. In
general, a Tarski sentence takes the form
is a logical predicate that may
additionally involve quantifiers on some or all of the variables. In
general, a Tarski sentence takes the form
