The inductive step to higher dimensions

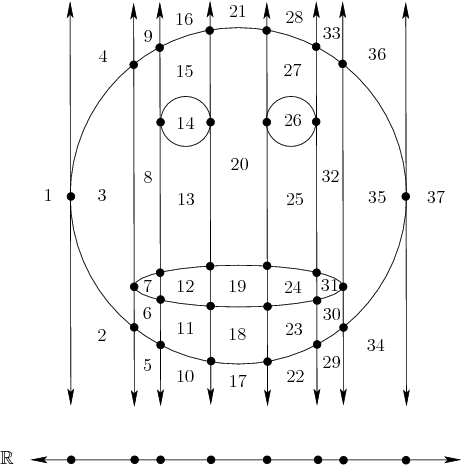
Now consider constructing a cylindrical algebraic decomposition for ${\mathbb{R}}^n$ (note the decomposition is actually semi-algebraic). Figure 6.35 shows an example for ${\mathbb{R}}^2$. First consider how to iteratively project the polynomials down to ${\mathbb{R}}$ to ensure that when the decomposition of ${\mathbb{R}}^n$ is constructed, the sign-invariant property is maintained. The resulting decomposition corresponds to a singular complex.

Figure 6.33: Critical points occur either when the surface folds over in the vertical direction or when surfaces intersect.

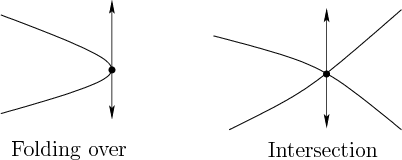There are two cases that cause cell boundaries to be formed, as shown in Figure 6.33. Let ${\cal F}_n$ denote the original set of polynomials in ${\mathbb{Q}}[x_1,\ldots, x_n]$ that are used to define the semi-algebraic set (or Tarski sentence) in ${\mathbb{R}}^n$. Form a single polynomial $f = \prod_{i=1}^m f_i$. Let $f^\prime = \partial f/\partial x_n$, which is also a polynomial. Let $g = GCD(f,f^\prime)$, which is the greatest common divisor of $f$ and $f^\prime$. The set of zeros of $g$ is the set of all points that are zeros of both $f$ and $f^\prime$. Being a zero of $f^\prime$ means that the surface given by $f = 0$ does not vary locally when perturbing $x_n$. These are places where a cell boundary needs to be formed because the surface may fold over itself in the $x_n$ direction, which is not permitted for a cylindrical decomposition. Another place where a cell boundary needs to be formed is at the intersection of two or more polynomials in ${\cal F}_n$. The projection technique from ${\mathbb{R}}^n$ to ${\mathbb{R}}^{n-1}$ generates a set, ${\cal F}_{n-1}$, of polynomials in ${\mathbb{Q}}[x_1,\ldots,x_{n-1}]$ that satisfies these requirements. The polynomials ${\cal F}_{n-1}$ have the property that at least one contains a zero point below every point in $x \in {\mathbb{R}}^n$ for which $f(x) = 0$ and $f^\prime(x)=0$, or polynomials in ${\cal F}_n$ intersect. The projection method that constructs ${\cal F}_{n-1}$ involves computing principle subresultant coefficients, which are covered in [77,853]. Resultants, of which the subresultants are an extension, are covered in [250].

The polynomials in ${\cal F}_{n-1}$ are then projected to ${\mathbb{R}}^{n-2}$ to obtain ${\cal F}_{n-2}$. This process continues until ${\cal F}_1$ is obtained, which is a set of polynomials in ${\mathbb{Q}}[x_1]$. A one-dimensional decomposition is formed, as defined earlier. From ${\cal F}_1$, a single polynomial is formed by taking the product, and ${\mathbb{R}}$ is partitioned into 0-cells and $1$-cells. We next describe the process of lifting a decomposition over ${\mathbb{R}}^{i-1}$ up to ${\mathbb{R}}^i$. This technique is applied iteratively until ${\mathbb{R}}^n$ is reached.

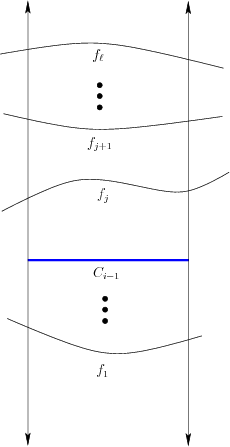
Assume inductively that a cylindrical algebraic decomposition has been computed for a set of polynomials ${\cal F}_{i-1}$ in ${\mathbb{Q}}[x_1,\ldots,x_{i-1}]$. The decomposition consists of $k$-cells for which $0 \leq k \leq i$. Let $p = (x_1,\ldots,x_{i-1}) \in {\mathbb{R}}^{i-1}$. For each one of the $k$-cells $C_{i-1}$, a cylinder over $C_{i-1}$ is defined as the $(k+1)$-dimensional set

$$\{ (p,x_i) \in {\mathbb{R}}^i \; \vert \; p \in C_{i-1} \} .$$ (6.23)

The cylinder is sliced into a strip of $k$-dimensional and $k+1$-dimensional cells by using polynomials in ${\cal F}_i$. Let $f_j$ denote one of the $\ell$ slicing polynomials in the cylinder, sorted in increasing $x_i$ order as $f_1$, $f_2$, $\ldots$, $f_j$, $f_{j+1}$, $\ldots$, $f_\ell$. The following kinds of cells are produced (see Figure 6.34):

1. Lower unbounded sector:

   $$\{ (p,x_i) \in {\mathbb{R}}^i \; \vert \; p \in C_{i-1} x_i < f_1(p) \} .$$ (6.24)

   
   

2. Section:

   $$\{ (p,x_i) \in {\mathbb{R}}^i \; \vert \; p \in C_{i-1} x_i = f_j(p) \} .$$ (6.25)

   
   

3. Bounded sector:

   $$\{ (p,x_i) \in {\mathbb{R}}^i \; \vert \; p \in C_{i-1} f_j(p) < x_i < f_{j+1}(p) \} .$$ (6.26)

   
   

4. Upper unbounded sector:

   $$\{ (p,x_i) \in {\mathbb{R}}^i \; \vert \; p \in C_{i-1} f_\ell(p) < x_i \} .$$ (6.27)

   
   

There is one degenerate possibility in which there are no slicing polynomials and the cylinder over $C_{i-1}$ can be extended into one unbounded cell. In general, the sample points are computed by picking a point in $p \in C_{i-1}$ and making a vertical column of samples of the form $(p,x_i)$. A polynomial in ${\mathbb{Q}}[x_i]$ can be generated, and the samples are placed using the same assignment technique that was used for the one-dimensional decomposition.

Figure 6.34: A cylinder over every $k$-cell $C_{i-1}$ is formed. A sequence of polynomials, $f_1$, $\ldots$, $f_\ell$, slices the cylinder into $k$-dimensional sections and $(k+1)$-dimensional sectors.

Figure 6.35: A cylindrical algebraic decomposition of the gingerbread face. There are $37$ $2$-cells, $64$ $1$-cells, and $28$ 0-cells. The straight $1$-cells are intervals of the vertical lines, and the curved ones are portions of the zero set of a polynomial in ${\cal F}$. The decomposition of ${\mathbb{R}}$ is also shown.

Example 6..6 (Mutilating the Gingerbread Face)   Figure 6.35 shows a cylindrical algebraic decomposition of the gingerbread face. Observe that the resulting complex is very similar to that obtained in Figure 6.19. $\blacksquare$

Note that the cells do not necessarily project onto a rectangular set, as in the case of a higher dimensional vertical decomposition. For example, a generic $n$-cell $C_n$ for a decomposition of ${\mathbb{R}}^n$ is described as the open set of $(x_1,\ldots, x_n) \in {\mathbb{R}}^n$ such that

 $&bull#bullet;$

$C_0 < x_n < C_0^\prime$ for some 0-cells $C_0,C_0^\prime \in {\mathbb{R}}$, which are roots of some $f,f^\prime \in {\cal F}_1$.

 $&bull#bullet;$

$(x_{n-1},x_n)$ lies between $C_1$ and $C^\prime_1$ for some $1$-cells $C_1$, $C_1^\prime$, which are zeros of some $f,f^\prime \in {\cal F}_2$.

$\vdots$

 $&bull#bullet;$

$(x_{n-i+1},\ldots,x_n)$ lies between $C_{i-1}$ and $C^\prime_{i-1}$ for some $i$-cells $C_{i-1}$, $C_{i-1}^\prime$, which are zeros of some $f,f^\prime \in {\cal F}_i$.

$\vdots$

 $&bull#bullet;$

$(x_1,\ldots,x_n)$ lies between $C_{n-1}$ and $C^\prime_{n-1}$ for some $(n-1)$-cells $C_{n-1}$, $C_{n-1}^\prime$, which are zeros of some $f,f^\prime \in {\cal F}_n$.

The resulting decomposition is sign invariant, which allows the decision and quantifier-elimination problems to be solved in finite time. To solve a decision problem, the polynomials in ${\cal F}_n$ are evaluated at every sample point to determine whether one of them satisfies the Tarski sentence. To solve the quantifier-elimination problem, note that any semi-algebraic sets that can be constructed from ${\cal F}_n$ can be defined as a union of some cells in the decomposition. For the given Tarski sentence, ${\cal F}_n$ is formed from all polynomials that are mentioned in the sentence, and the cell decomposition is performed. Once obtained, the sign information is used to determine which cells need to be included in the union. The resulting union of cells is designed to include only the points in ${\mathbb{R}}^n$ at which the Tarski sentence is TRUE.