
Next: Hardness and completeness Up: 6.5.1 Lower Bounds Previous: 6.5.1 Lower Bounds
A language is a set of binary strings associated with a problem. It represents the complete set of instances of a problem. An algorithm is said to decide a language if in finite time it correctly accepts all strings that belong to it and rejects all others. The interesting question is: How much time or space is required to decide a language? This question is asked of the problem, under the assumption that the best possible algorithm would be used to decide it. (We can easily think of inefficient algorithms that waste resources.)
A complexity class is a set of languages that can all be decided
within some specified resource bound. The class P is the set of all
languages (and hence problems) for which a polynomial-time algorithm
exists (i.e., the algorithm runs in time ![]() for some integer
for some integer
![]() ). By definition, an algorithm is called efficient if it decides its associated
language in polynomial time.6.7 If no
efficient algorithm exists, then the problem is called intractable. The relationship between
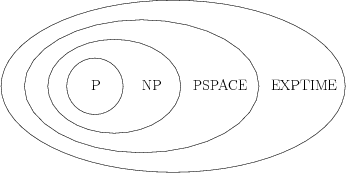
several other classes that often emerge in theoretical motion planning
is shown in Figure 6.40. The class NP is the set of languages that can be solved in
polynomial time by a nondeterministic Turing machine. Some
discussion of nondeterministic machines appears in Section
11.3.2. Intuitively, it means that solutions can be verified
in polynomial time because the machine magically knows which choices
to make while trying to make the decision. The class PSPACE is
the set of languages that can be decided with no more than a
polynomial amount of storage space during the execution of the
algorithm (NPSPACE
). By definition, an algorithm is called efficient if it decides its associated
language in polynomial time.6.7 If no
efficient algorithm exists, then the problem is called intractable. The relationship between
several other classes that often emerge in theoretical motion planning
is shown in Figure 6.40. The class NP is the set of languages that can be solved in
polynomial time by a nondeterministic Turing machine. Some
discussion of nondeterministic machines appears in Section
11.3.2. Intuitively, it means that solutions can be verified
in polynomial time because the machine magically knows which choices
to make while trying to make the decision. The class PSPACE is
the set of languages that can be decided with no more than a
polynomial amount of storage space during the execution of the
algorithm (NPSPACE![]() PSPACE, so there is no nondeterministic version).
The class EXPTIME is the set of languages that can be decided in
time
PSPACE, so there is no nondeterministic version).
The class EXPTIME is the set of languages that can be decided in
time
![]() for some integer
for some integer ![]() . It is known that EXPTIME is
larger than P, but it is not known precisely where the boundaries of
NP and PSPACE lie. It might be the case that P = NP = PSPACE
(although hardly anyone believes this), or it could be that NP =
PSPACE = EXPTIME.
. It is known that EXPTIME is
larger than P, but it is not known precisely where the boundaries of
NP and PSPACE lie. It might be the case that P = NP = PSPACE
(although hardly anyone believes this), or it could be that NP =
PSPACE = EXPTIME.
 |
Steven M LaValle 2012-04-20