
Next: Fixed-roadmap coordination Up: 7.2.2 Decoupled planning Previous: Prioritized planning
Suppose that each robot
![]() is constrained to follow a path
is constrained to follow a path
![]() , which can be computed using
any ordinary motion planning technique. For
, which can be computed using
any ordinary motion planning technique. For ![]() robots, an
robots, an
![]() -dimensional state space called a coordination space is
defined that schedules the motions of the robots along their paths so
that they will not collide [746]. One important feature is
that time will only be implicitly represented in the
coordination space. An algorithm must compute a path in the
coordination space, from which explicit timings can be easily
extracted.
-dimensional state space called a coordination space is
defined that schedules the motions of the robots along their paths so
that they will not collide [746]. One important feature is
that time will only be implicitly represented in the
coordination space. An algorithm must compute a path in the
coordination space, from which explicit timings can be easily
extracted.
For ![]() robots, the coordination space
robots, the coordination space ![]() is defined as the
is defined as the
![]() -dimensional unit cube
-dimensional unit cube
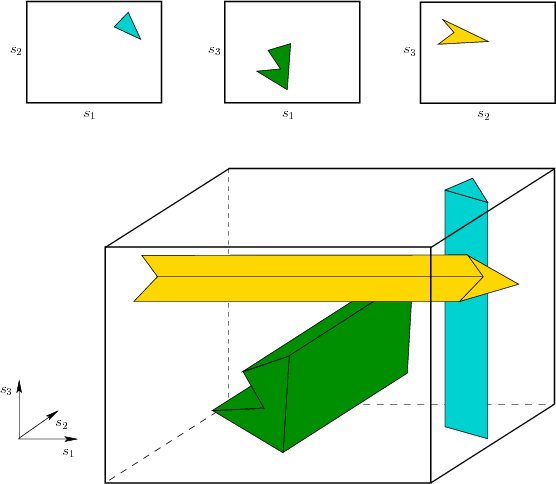
![]() . Figure 7.9
depicts an example for which
. Figure 7.9
depicts an example for which ![]() . The
. The ![]() th coordinate of
th coordinate of ![]() represents the domain,
represents the domain,
![]() , of the path
, of the path ![]() . Let
. Let ![]() denote a point in
denote a point in ![]() (it is also the
(it is also the ![]() th component of
th component of ![]() ). A
state,
). A
state, ![]() , indicates the configuration of every robot. For
each
, indicates the configuration of every robot. For
each ![]() , the configuration
, the configuration
![]() is given by
is given by
![]() . At state
. At state
![]() , every robot is in its
initial configuration,
, every robot is in its
initial configuration,
![]() , and at state
, and at state
![]() , every robot is in its goal configuration,
, every robot is in its goal configuration,
![]() . Any continuous path,
. Any continuous path,
![]() , for which
, for which
![]() and
and
![]() , moves the robots to their goal configurations. The
path
, moves the robots to their goal configurations. The
path ![]() does not even need to be monotonic, in contrast to
prioritized planning.
does not even need to be monotonic, in contrast to
prioritized planning.
 |
One important concern has been neglected so far. What prevents us
from designing ![]() as a straight-line path between the opposite
corners of
as a straight-line path between the opposite
corners of ![]() ? We have not yet taken into account the
collisions between the robots. This forms an obstacle region
? We have not yet taken into account the
collisions between the robots. This forms an obstacle region
![]() that must be avoided when designing a path through
that must be avoided when designing a path through ![]() .
Thus, the task is to design
.
Thus, the task is to design
![]() , in
which
, in
which
![]() .
.
The definition of ![]() is very similar to (7.8)
and (7.10), except that here the state-space dimension
is much smaller. Each
is very similar to (7.8)
and (7.10), except that here the state-space dimension
is much smaller. Each ![]() is replaced by a single parameter. The
cylindrical structure, however, is still retained, as shown in Figure
7.9. Each cylinder of
is replaced by a single parameter. The
cylindrical structure, however, is still retained, as shown in Figure
7.9. Each cylinder of ![]() is
is
Standard motion planning algorithms can be applied to the coordination
space because there is no monotonicity requirement on ![]() . If
1)
. If
1)
![]() , 2)
, 2) ![]() (two robots), 3) the obstacles and robots
are polygonal, and 4) the paths,
(two robots), 3) the obstacles and robots
are polygonal, and 4) the paths, ![]() , are piecewise-linear, then
, are piecewise-linear, then
![]() is a polygonal region in
is a polygonal region in ![]() . This enables the methods of
Section 6.2, for a polygonal
. This enables the methods of
Section 6.2, for a polygonal
![]() , to directly apply
after the representation of
, to directly apply
after the representation of ![]() is explicitly constructed. For
is explicitly constructed. For ![]() , the multi-dimensional version of vertical cell decomposition
given for
, the multi-dimensional version of vertical cell decomposition
given for ![]() in Section 6.3.3 can be applied. For
general coordination problems, cylindrical algebraic
decomposition or Canny's roadmap algorithm can be applied. For
the problem of robots in
in Section 6.3.3 can be applied. For
general coordination problems, cylindrical algebraic
decomposition or Canny's roadmap algorithm can be applied. For
the problem of robots in
![]() that either translate or move
along circular paths, a resolution complete planning method based on
the exact determination of
that either translate or move
along circular paths, a resolution complete planning method based on
the exact determination of ![]() using special collision detection
methods is given in [886].
using special collision detection
methods is given in [886].
For very challenging coordination problems, sampling-based solutions
may yield practical solutions. Perhaps one of the simplest solutions
is to place a grid over ![]() and adapt the classical search algorithms,
as described in Section 5.4.2 [606,746].
Other possibilities include using the RDTs of Section 5.5 or, if the multiple-query framework is
appropriate, then the sampling-based roadmap methods of
5.6 are suitable. Methods for validating the path
segments, which were covered in Section 5.3.4, can be
adapted without trouble to the case of coordination spaces.
and adapt the classical search algorithms,
as described in Section 5.4.2 [606,746].
Other possibilities include using the RDTs of Section 5.5 or, if the multiple-query framework is
appropriate, then the sampling-based roadmap methods of
5.6 are suitable. Methods for validating the path
segments, which were covered in Section 5.3.4, can be
adapted without trouble to the case of coordination spaces.
Thus far, the particular speeds of the robots have been neglected.
For explanation purposes, consider the case of ![]() . Moving
vertically or horizontally in
. Moving
vertically or horizontally in ![]() holds one robot fixed while the
other moves at some maximum speed. Moving diagonally in
holds one robot fixed while the
other moves at some maximum speed. Moving diagonally in ![]() moves
both robots, and their relative speeds depend on the slope of the
path. To carefully regulate these speeds, it may be necessary to
reparameterize the paths by distance. In this case each axis of
moves
both robots, and their relative speeds depend on the slope of the
path. To carefully regulate these speeds, it may be necessary to
reparameterize the paths by distance. In this case each axis of ![]() represents the distance traveled, instead of
represents the distance traveled, instead of ![]() .
.
Steven M LaValle 2012-04-20