
Next: Planning on the cube Up: 7.2.2 Decoupled planning Previous: Fixed-roadmap coordination
How is the coordination space represented when there are multiple
paths for each robot? It turns out that a cube complex is
obtained, which is a special kind of singular complex (recall from
Section 6.3.1). The coordination space for ![]() fixed
paths can be considered as a singular
fixed
paths can be considered as a singular ![]() -simplex. For example, the
problem in Figure 7.9 can be considered as a singular
-simplex. For example, the
problem in Figure 7.9 can be considered as a singular
![]() -simplex,
-simplex,
![]() . In Section 6.3.1,
the domain of a
. In Section 6.3.1,
the domain of a ![]() -simplex was defined using
-simplex was defined using ![]() , a
, a ![]() -dimensional
ball; however, a cube,
-dimensional
ball; however, a cube, ![]() , also works because
, also works because ![]() and
and
![]() are homeomorphic.
are homeomorphic.
For a topological space, ![]() , let a
, let a ![]() -cube (which is also a
singular
-cube (which is also a
singular ![]() -simplex),
-simplex),
![]() , be a continuous mapping
, be a continuous mapping
![]() . A cube complex is obtained by connecting
together
. A cube complex is obtained by connecting
together ![]() -cubes of different dimensions. Every
-cubes of different dimensions. Every ![]() -cube for
-cube for ![]() has
has ![]() faces, which are
faces, which are ![]() -cubes that are
obtained as follows. Let
-cubes that are
obtained as follows. Let
![]() denote a point in
denote a point in
![]() . For each
. For each
![]() , one face is obtained by
setting
, one face is obtained by
setting ![]() and another is obtained by setting
and another is obtained by setting ![]() .
.
The cubes must fit together nicely, much in the same way that the
simplexes of a simplicial complex were required to fit together. To
be a cube complex, ![]() must be a collection of simplexes
that satisfy the following requirements:
must be a collection of simplexes
that satisfy the following requirements:
Let
![]() denote a topological graph (which may also be a
roadmap) for robot
denote a topological graph (which may also be a
roadmap) for robot
![]() . The graph edges are paths of the form
. The graph edges are paths of the form
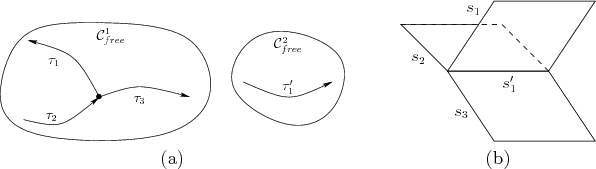
![]() . Before covering formal
definitions of the resulting complex, consider Figure
7.10a, in which
. Before covering formal
definitions of the resulting complex, consider Figure
7.10a, in which
![]() moves along three paths
connected in a ``T'' junction and
moves along three paths
connected in a ``T'' junction and
![]() moves along one path. In
this case, three 2D fixed-path coordination spaces are attached
together along one common edge, as shown in Figure
7.10b. The resulting cube complex is defined by three
moves along one path. In
this case, three 2D fixed-path coordination spaces are attached
together along one common edge, as shown in Figure
7.10b. The resulting cube complex is defined by three
![]() -cubes (i.e., squares), one
-cubes (i.e., squares), one ![]() -cube (i.e., line segment), and
eight 0-cubes (i.e., corner points).
-cube (i.e., line segment), and
eight 0-cubes (i.e., corner points).
 |
Now suppose more generally that there are two robots,
![]() and
and
![]() , with associated topological graphs,
, with associated topological graphs,
![]() and
and
![]() , respectively. Suppose that
, respectively. Suppose that ![]() and
and
![]() have
have ![]() and
and ![]() edges, respectively. A 2D cube
complex,
edges, respectively. A 2D cube
complex, ![]() , is obtained as follows. Let
, is obtained as follows. Let ![]() denote the
denote the
![]() th path of
th path of
![]() , and let
, and let ![]() denote the
denote the ![]() th path
of
th path
of
![]() . A
. A ![]() -cube (square) exists in
-cube (square) exists in ![]() for every way to
select an edge from each graph. Thus, there are
for every way to
select an edge from each graph. Thus, there are ![]()
![]() -cubes,
one for each pair
-cubes,
one for each pair
![]() , such that
, such that
![]() and
and
![]() . The
. The ![]() -cubes are generated for pairs of the form
-cubes are generated for pairs of the form
![]() for
for
![]() and
and
![]() , or
, or
![]() for
for
![]() and
and
![]() . The 0-cubes
(corner points) are reached for each pair
. The 0-cubes
(corner points) are reached for each pair ![]() such that
such that
![]() and
and
![]() .
.
If there are ![]() robots, then an
robots, then an ![]() -dimensional cube complex arises.
Every
-dimensional cube complex arises.
Every ![]() -cube corresponds to a unique combination of paths, one for
each robot. The
-cube corresponds to a unique combination of paths, one for
each robot. The ![]() -cubes are the faces of the
-cubes are the faces of the ![]() -cubes. This
continues iteratively until the 0-cubes are reached.
-cubes. This
continues iteratively until the 0-cubes are reached.
Steven M LaValle 2012-04-20