The RDT algorithm given Figure 5.21 can be applied
directly; however, the STOPPING-CONFIGURATION function in line 4
must be changed to account for both obstacles and the constraints that
define
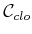 . Figure 7.22 shows one general approach
that is based on numerical continuation [18]. An
alternative is to use inverse kinematics, which is part of the
approach described in Section 7.4.2. The nearest RDT
vertex,
. Figure 7.22 shows one general approach
that is based on numerical continuation [18]. An
alternative is to use inverse kinematics, which is part of the
approach described in Section 7.4.2. The nearest RDT
vertex,
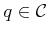 , to the sample
, to the sample
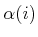 is first computed. Let
is first computed. Let
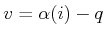 , which indicates the direction in which an edge
would be made from
, which indicates the direction in which an edge
would be made from 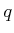 if there were no constraints. A local motion
is then computed by projecting
if there were no constraints. A local motion
is then computed by projecting 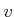 into the tangent
plane7.3 of
into the tangent
plane7.3 of
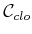 at the point
at the point 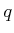 . Since
. Since
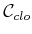 is
generally nonlinear, the local motion produces a point that is not
precisely on
is
generally nonlinear, the local motion produces a point that is not
precisely on
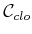 . Some numerical tolerance is generally accepted,
and a small enough step is taken to ensure that the tolerance is
maintained. The process iterates by computing
. Some numerical tolerance is generally accepted,
and a small enough step is taken to ensure that the tolerance is
maintained. The process iterates by computing 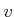 with respect to the
new point and moving in the direction of
with respect to the
new point and moving in the direction of 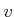 projected into the new
tangent plane. If the error threshold is surpassed, then motions must
be executed in the normal direction to return to
projected into the new
tangent plane. If the error threshold is surpassed, then motions must
be executed in the normal direction to return to
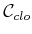 . This
process of executing tangent and normal motions terminates when
progress can no longer be made, due either to the alignment of the
tangent plane (nearly perpendicular to
. This
process of executing tangent and normal motions terminates when
progress can no longer be made, due either to the alignment of the
tangent plane (nearly perpendicular to 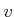 ) or to an obstacle. This
finally yields
) or to an obstacle. This
finally yields 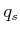 , the stopping configuration. The new path
followed in
, the stopping configuration. The new path
followed in
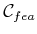 is no longer a ``straight line'' as was possible
for some problems in Section 5.5; therefore, the approximate
methods in Section 5.5.2 should be used to create
intermediate vertices along the path.
is no longer a ``straight line'' as was possible
for some problems in Section 5.5; therefore, the approximate
methods in Section 5.5.2 should be used to create
intermediate vertices along the path.
In each iteration, the tangent plane computation is computed at some
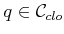 as follows. The differential configuration vector
as follows. The differential configuration vector 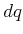 lies in the tangent space of a constraint
lies in the tangent space of a constraint
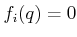 if
if
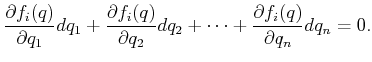 |
(7.22) |
This leads to the following homogeneous system for all of the 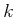 polynomials in
polynomials in 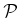 that define the closure constraints
that define the closure constraints
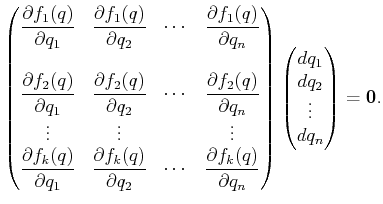 |
(7.23) |
If the rank of the matrix is 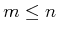 , then
, then 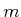 configuration
displacements can be chosen independently, and the remaining
configuration
displacements can be chosen independently, and the remaining 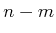 parameters must satisfy (7.23). This can be
solved using linear algebra techniques, such as singular value
decomposition (SVD) [399,961], to compute an orthonormal basis
for the tangent space at
parameters must satisfy (7.23). This can be
solved using linear algebra techniques, such as singular value
decomposition (SVD) [399,961], to compute an orthonormal basis
for the tangent space at 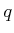 . Let
. Let 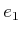 ,
, 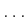 ,
, 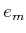 , denote
these
, denote
these 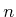 -dimensional basis vectors. The components of the motion
direction are obtained from
-dimensional basis vectors. The components of the motion
direction are obtained from
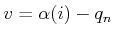 . First, construct
the inner products,
. First, construct
the inner products,
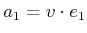 ,
,
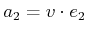 ,
,
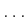 ,
,
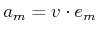 . Using these, the projection of
. Using these, the projection of 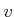 in
the tangent plane is the
in
the tangent plane is the 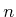 -dimensional vector
-dimensional vector 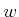 given by
given by
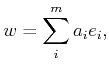 |
(7.24) |
which is used as the direction of motion. The magnitude must be
appropriately scaled to take sufficiently small steps. Since
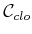 is generally curved, a linear motion leaves
is generally curved, a linear motion leaves
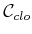 . A motion
in the inward normal direction is then required to move back onto
. A motion
in the inward normal direction is then required to move back onto
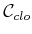 .
.
Since the dimension 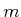 of
of
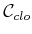 is less than
is less than 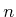 , the procedure
just described can only produce numerical approximations to paths in
, the procedure
just described can only produce numerical approximations to paths in
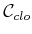 . This problem also arises in implicit curve tracing in
graphics and geometric modeling [454]. Therefore, each
constraint
. This problem also arises in implicit curve tracing in
graphics and geometric modeling [454]. Therefore, each
constraint
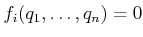 is actually slightly weakened to
is actually slightly weakened to
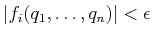 for some fixed tolerance
for some fixed tolerance
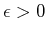 . This essentially ``thickens''
. This essentially ``thickens''
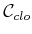 so that its dimension is
so that its dimension is
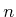 . As an alternative to computing the tangent plane, motion
directions can be sampled directly inside of this thickened region
without computing tangent planes. This results in an easier
implementation, but it is less efficient [979].
. As an alternative to computing the tangent plane, motion
directions can be sampled directly inside of this thickened region
without computing tangent planes. This results in an easier
implementation, but it is less efficient [979].
Steven M LaValle
2012-04-20

![]() as follows. The differential configuration vector
as follows. The differential configuration vector ![]() lies in the tangent space of a constraint
lies in the tangent space of a constraint
![]() if
if
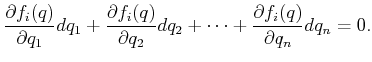
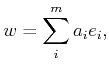
![]() of
of
![]() is less than
is less than ![]() , the procedure
just described can only produce numerical approximations to paths in
, the procedure
just described can only produce numerical approximations to paths in
![]() . This problem also arises in implicit curve tracing in
graphics and geometric modeling [454]. Therefore, each
constraint
. This problem also arises in implicit curve tracing in
graphics and geometric modeling [454]. Therefore, each
constraint
![]() is actually slightly weakened to
is actually slightly weakened to
![]() for some fixed tolerance
for some fixed tolerance
![]() . This essentially ``thickens''
. This essentially ``thickens''
![]() so that its dimension is
so that its dimension is
![]() . As an alternative to computing the tangent plane, motion
directions can be sampled directly inside of this thickened region
without computing tangent planes. This results in an easier
implementation, but it is less efficient [979].
. As an alternative to computing the tangent plane, motion
directions can be sampled directly inside of this thickened region
without computing tangent planes. This results in an easier
implementation, but it is less efficient [979].