
Next: Loop generator Up: 7.4.2 Active-Passive Link Decompositions Previous: 7.4.2 Active-Passive Link Decompositions
 |
 |
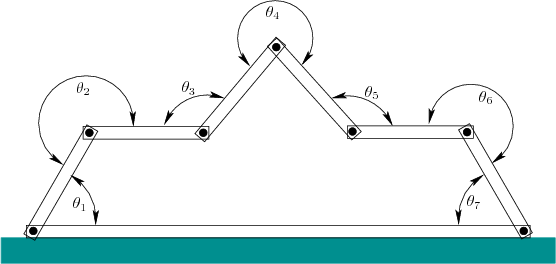
Temporarily, suppose that the linkage forms a single loop as shown in
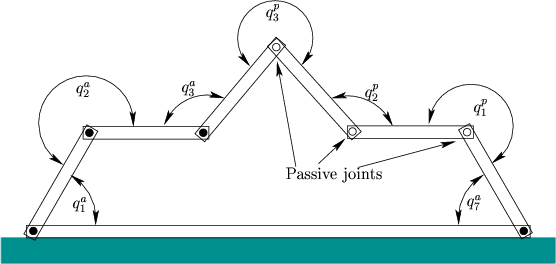
Figure 7.23. One possible decomposition into active ![]() and passive
and passive ![]() variables is given in Figure 7.24. If
constrained to form a loop, the linkage has four degrees of freedom,
assuming the bottom link is rigidly attached to the ground. This
means that values can be chosen for four active joint angles
variables is given in Figure 7.24. If
constrained to form a loop, the linkage has four degrees of freedom,
assuming the bottom link is rigidly attached to the ground. This
means that values can be chosen for four active joint angles ![]() and
the remaining three
and
the remaining three ![]() can be derived from solving the inverse
kinematics. To determine
can be derived from solving the inverse
kinematics. To determine ![]() , there are three equations and three
unknowns. Unfortunately, these equations are nonlinear and fairly
complicated. Nevertheless, efficient solutions exist for this case,
and the 3D generalization [675]. For a 3D loop formed of
revolute joints, there are six passive variables. The number,
, there are three equations and three
unknowns. Unfortunately, these equations are nonlinear and fairly
complicated. Nevertheless, efficient solutions exist for this case,
and the 3D generalization [675]. For a 3D loop formed of
revolute joints, there are six passive variables. The number, ![]() , of
passive links in
, of
passive links in
![]() and the number
and the number ![]() for
for
![]() arise from the
dimensions of
arise from the
dimensions of ![]() and
and ![]() , respectively. This is the freedom
that is stripped away from the system by enforcing the closure
constraints. Methods for efficiently computing inverse kinematics in
two and three dimensions are given in [30]. These can also be
applied to the RDT stepping method in Section 7.4.1,
instead of using continuation.
, respectively. This is the freedom
that is stripped away from the system by enforcing the closure
constraints. Methods for efficiently computing inverse kinematics in
two and three dimensions are given in [30]. These can also be
applied to the RDT stepping method in Section 7.4.1,
instead of using continuation.
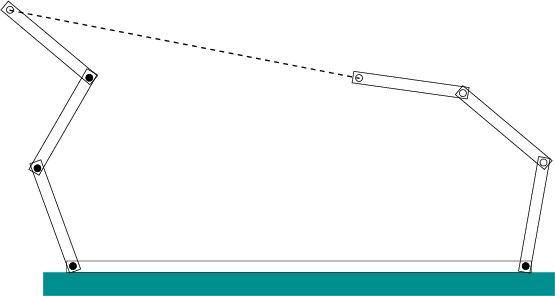 |
If the maximal number of passive variables is used, there is at most a
finite number of solutions to the inverse kinematics problem; this
implies that there are often several choices for the passive variable
values. It could be the case that for some assignments of active
variables, there are no solutions to the inverse kinematics. An
example is depicted in Figure 7.25. Suppose that we want
to generate samples in
![]() by selecting random values for
by selecting random values for ![]() and then using inverse kinematics for
and then using inverse kinematics for ![]() . What is the probability
that a solution to the inverse kinematics exists? For the example
shown, it appears that solutions would not exist in most trials.
. What is the probability
that a solution to the inverse kinematics exists? For the example
shown, it appears that solutions would not exist in most trials.
Steven M LaValle 2012-04-20