Drug design

Figure 7.32: A pharmacophore is a model used by chemists to simplify the interaction process between a ligand (candidate drug molecule) and a protein. It often amounts to holding certain features of the molecule fixed in ${\mathbb{R}}^3$. In this example, the positions of three atoms must be fixed relative to the body frame of an arbitrarily designated root atom. It is assumed that these features interact with some complementary features in the cavity of the protein.

A sampling-based motion planning approach to pharmaceutical drug design is taken in [601]. The development of a drug is a long, incremental process, typically requiring years of research and experimentation. The goal is to find a relatively small molecule called a ligand, typically comprising a few dozen atoms, that docks with a receptor cavity in a specific protein [615]; Figure 1.14 (Section 1.2) illustrated this. Examples of drug molecules were also given in Figure 1.14. Protein-ligand docking can stimulate or inhibit some biological activity, ultimately leading to the desired pharmacological effect. The problem of finding suitable ligands is complicated due to both energy considerations and the flexibility of the ligand. In addition to satisfying structural considerations, factors such as synthetic accessibility, drug pharmacology and toxicology greatly complicate and lengthen the search for the most effective drug molecules.

Figure 7.33: The modeling of a flexible molecule is similar to that of a robot. One atom is designated as the root, and the remaining bodies are arranged in a tree. If there are cyclic chains in the molecules, then constraints as described in Section 4.4 must be enforced. Typically, only some bonds are capable of rotation, whereas others must remain rigid.

One popular model used by chemists in the context of drug design is a pharmacophore, which serves as a template for the desired ligand [229,339,383,860]. The pharmacophore is expressed as a set of features that an effective ligand should possess and a set of spatial constraints among the features. Examples of features are specific atoms, centers of benzene rings, positive or negative charges, hydrophobic or hydrophilic centers, and hydrogen bond donors or acceptors. Features generally require that parts of the molecule must remain fixed in ${\mathbb{R}}^3$, which induces kinematic closure constraints. These features are developed by chemists to encapsulate the assumption that ligand binding is due primarily to the interaction of some features of the ligand to ``complementary" features of the receptor. The interacting features are included in the pharmacophore, which is a template for screening candidate drugs, and the rest of the ligand atoms merely provide a scaffold for holding the pharmacophore features in their spatial positions. Figure 7.32 illustrates the pharmacophore concept.

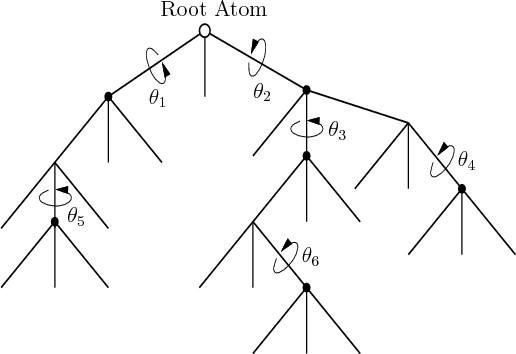
Candidate drug molecules (ligands), such as the ones shown in Figure 1.14, can be modeled as a tree of bodies as shown in Figure 7.33. Some bonds can rotate, yielding revolute joints in the model; other bonds must remain fixed. The drug design problem amounts to searching the space of configurations (called conformations) to try to find a low-energy configuration that also places certain atoms in specified locations in ${\mathbb{R}}^3$. This additional constraint arises from the pharmacophore and causes the planning to occur on ${{\cal C}_{clo}}$ from Section 7.4 because the pharmacophores can be expressed as closure constraints.

An energy function serves a purpose similar to that of a collision detector. The evaluation of a ligand for drug design requires determining whether it can achieve low-energy conformations that satisfy the pharmacophore constraints. Thus, the task is different from standard motion planning in that there is no predetermined goal configuration. One of the greatest difficulties is that the energy functions are extremely complicated, nonlinear, and empirical. Here is typical example (used in [601]):

$$\begin{tabular}{ll} $e(q)$=& $ \sum_{bonds}{{1 \over 2} K_b (R- R... ... \right] + { {c_i c_j} \over {\epsilon r_{ij} }}} \right\}. $ \end{tabular}$$ (7.25)

The energy accounts for torsion-angle deformations, van der Waals potential, and Coulomb potentials. In (7.25), the first sum is taken over all bonds, the second over all bond angles, the third over all rotatable bonds, and the last is taken over all pairs of atoms. The variables are the force constants, $K_b, K_a$, and $K_d$; the dielectric constant, $\epsilon$; a periodicity constant, $p$; the Lennard-Jones radii, $\sigma_{ij}$; well depth, $\epsilon_{ij}$; partial charge, $c_i$; measured bond length, $R$; equilibrium bond length, $R^\prime$; measured bond angle, $\alpha$; equilibrium bond angle, $\alpha^\prime$; measured torsional angle, $\theta$; equilibrium torsional angle, $\theta^\prime$; and distance between atom centers, $r_{ij}$. Although the energy expression is very complicated, it only depends on the configuration variables; all others are constants that are estimated in advance.