
Next: 8.4.4 A Step Toward Up: 8.4 Complete Methods for Previous: 8.4.2 Vector Fields Over
The vector fields developed in the last section yield feasible
trajectories, but not necessarily optimal trajectories unless the
initial and goal states are in the same convex ![]() -cell. If
-cell. If
![]() , then it is possible to make a continuous version of
Dijkstra's algorithm [708]. This results in an exact
cost-to-go function over
, then it is possible to make a continuous version of
Dijkstra's algorithm [708]. This results in an exact
cost-to-go function over ![]() based on the Euclidean shortest
path to a goal,
based on the Euclidean shortest
path to a goal, ![]() . The cost-to-go function serves as the
navigation function, from which the feedback plan is defined by using
a local steepest descent.
. The cost-to-go function serves as the
navigation function, from which the feedback plan is defined by using
a local steepest descent.
Suppose that ![]() is bounded by a simple polygon (no holes). Assume
that only normalized vector fields are allowed. The cost functional
is assumed to be the Euclidean distance traveled along a state
trajectory. Recall from Section 6.2.4 that for optimal
path planning,
is bounded by a simple polygon (no holes). Assume
that only normalized vector fields are allowed. The cost functional
is assumed to be the Euclidean distance traveled along a state
trajectory. Recall from Section 6.2.4 that for optimal
path planning,
![]() must be used. Assume that
must be used. Assume that
![]() and
and
![]() have the same connectivity.8.12 This technically interferes with
the definition of tangent spaces from Section 8.3
because each point of
have the same connectivity.8.12 This technically interferes with
the definition of tangent spaces from Section 8.3
because each point of ![]() must be contained in an open neighborhood.
Nevertheless, we allow vectors along the boundary, provided that they
``point'' in a direction tangent to the boundary. This can be
formally defined by considering boundary regions as separate
manifolds.
must be contained in an open neighborhood.
Nevertheless, we allow vectors along the boundary, provided that they
``point'' in a direction tangent to the boundary. This can be
formally defined by considering boundary regions as separate
manifolds.
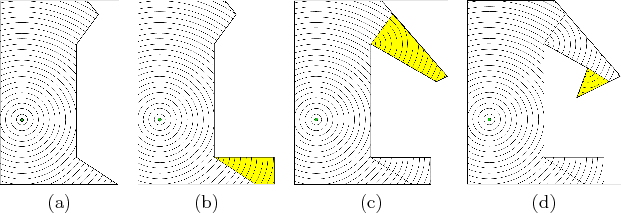 |
Consider computing the optimal cost-to-go to a point ![]() for a problem such as that shown in Figure 8.12a. For any
for a problem such as that shown in Figure 8.12a. For any
![]() , let the visibility polygon
, let the visibility polygon ![]() refer to the set
of all points visible from
refer to the set
of all points visible from ![]() , which is illustrated in Figure
8.12b. A point
, which is illustrated in Figure
8.12b. A point ![]() lies in
lies in ![]() if and only if the
line segment from
if and only if the
line segment from ![]() to
to ![]() is contained in
is contained in ![]() . This implies that
the cost-to-go from
. This implies that
the cost-to-go from ![]() to
to ![]() is just the Euclidean distance from
is just the Euclidean distance from
![]() to
to ![]() . The optimal navigation function can therefore be
immediately defined over
. The optimal navigation function can therefore be
immediately defined over
![]() as
as
| (8.42) |
How do we compute the optimal cost-to-go values for the points
in
![]() ? For the segments on the boundary of
? For the segments on the boundary of
![]() for any
for any ![]() , some edges are contained in the boundary of
, some edges are contained in the boundary of
![]() , and others cross the interior of
, and others cross the interior of ![]() . For the example in Figure
8.12b, there are two edges that cross the interior. For
each segment that crosses the interior, let the closer of the two
vertices to
. For the example in Figure
8.12b, there are two edges that cross the interior. For
each segment that crosses the interior, let the closer of the two
vertices to ![]() be referred to as a way point. Two way points
are indicated in Figure 8.12b. The way points of
be referred to as a way point. Two way points
are indicated in Figure 8.12b. The way points of
![]() are places through which some optimal paths must cross.
Let
are places through which some optimal paths must cross.
Let ![]() for any
for any ![]() denote the set of way points of
denote the set of way points of ![]() .
.
A straightforward algorithm proceeds as follows. Let ![]() denote the
set of points over which
denote the
set of points over which ![]() has been defined, in the
has been defined, in the ![]() th
iteration of the algorithm. In the first iteration,
th
iteration of the algorithm. In the first iteration,
![]() , which is the case shown in Figure 8.13a.
The way points of
, which is the case shown in Figure 8.13a.
The way points of
![]() are placed in a queue,
are placed in a queue, ![]() . In each
following iteration, a way point
. In each
following iteration, a way point ![]() is removed from
is removed from ![]() . Let
. Let ![]() denote the domain over which
denote the domain over which ![]() is defined so far. The domain of
is defined so far. The domain of
![]() is extended to include all new points visible from
is extended to include all new points visible from ![]() . These
new points are
. These
new points are
![]() . This yields
. This yields
![]() , the extended domain of
, the extended domain of ![]() . The values of
. The values of ![]() for
for
![]() are defined by
are defined by
| (8.43) |
The visibility polygon can be computed in time
![]() if
if ![]() is
described by
is
described by ![]() edges. This is accomplished by performing a
radial sweep, which is
an adaptation of the method applied in Section 6.2.2 for
vertical cell decomposition. The difference for computing
edges. This is accomplished by performing a
radial sweep, which is
an adaptation of the method applied in Section 6.2.2 for
vertical cell decomposition. The difference for computing ![]() is
that a ray anchored at
is
that a ray anchored at ![]() is swept radially (like a radar sweep).
The segments that intersect the ray are sorted by their distance from
is swept radially (like a radar sweep).
The segments that intersect the ray are sorted by their distance from
![]() . For the algorithm that constructs the navigation function, no
more than
. For the algorithm that constructs the navigation function, no
more than ![]() visibility polygons are computed because each one is
computed from a unique way point. This implies
visibility polygons are computed because each one is
computed from a unique way point. This implies
![]() running
time for the whole algorithm. Unfortunately, there is no extension to
higher dimensions; recall from Section 7.7.1 that computing
shortest paths in a 3D environment is NP-hard [172].
running
time for the whole algorithm. Unfortunately, there is no extension to
higher dimensions; recall from Section 7.7.1 that computing
shortest paths in a 3D environment is NP-hard [172].
The algorithm given here is easy to describe, but it is not the most
general, nor the most efficient. If ![]() has holes, then the level set
curves can collide by arriving from different directions when
traveling around an obstacle. The queue,
has holes, then the level set
curves can collide by arriving from different directions when
traveling around an obstacle. The queue, ![]() , described above can be
sorted as in Dijkstra's algorithm, and special data structures
are needed to identify when critical events occur as the
cost-to-go is propagated outward. It was shown in
[443] that this can be done in time
, described above can be
sorted as in Dijkstra's algorithm, and special data structures
are needed to identify when critical events occur as the
cost-to-go is propagated outward. It was shown in
[443] that this can be done in time
![]() and space
and space
![]() .
.
Steven M LaValle 2012-04-20