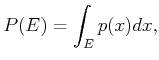A probability space is a three-tuple,
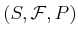 , in which
the three components are
, in which
the three components are
- Sample space: A nonempty set
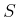 called the sample
space, which represents
all possible outcomes.
called the sample
space, which represents
all possible outcomes.
- Event space: A collection
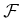 of subsets of
of subsets of 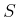 ,
called the event space. If
,
called the event space. If 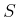 is discrete, then usually
is discrete, then usually
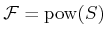 . If
. If 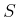 is continuous, then
is continuous, then 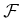 is usually a sigma-algebra
on
is usually a sigma-algebra
on 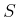 , as defined in Section 5.1.3.
, as defined in Section 5.1.3.
- Probability function: A
function,
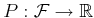 , that assigns probabilities to
the events in
, that assigns probabilities to
the events in 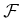 . This will sometimes be referred to as a probability distribution over
. This will sometimes be referred to as a probability distribution over 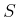 .
.
The probability function, 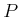 , must satisfy several basic axioms:
, must satisfy several basic axioms:
-
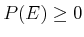 for all
for all
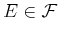 .
.
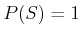 .
.
-
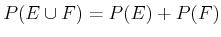 if
if
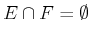 , for all
, for all
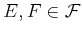 .
.
If 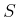 is discrete, then the definition of
is discrete, then the definition of 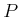 over all of
over all of 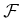 can
be inferred from its definition on single elements of
can
be inferred from its definition on single elements of 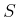 by using the
axioms. It is common in this case to write
by using the
axioms. It is common in this case to write 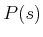 for some
for some 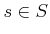 ,
which is slightly abusive because
,
which is slightly abusive because 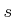 is not an event. It technically
should be
is not an event. It technically
should be 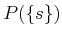 for some
for some
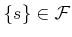 .
.
Example 9..4 (Tossing a Die)
Consider tossing a six-sided cube or die that has numbers
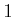
to
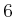
painted on its sides. When the die comes to rest, it will always show
one number. In this case,
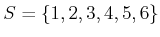
is the sample space.
The event space is
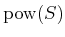
, which is all
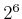
subsets of
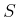
.
Suppose that the probability function is assigned to indicate that all
numbers are equally likely. For any individual
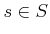
,
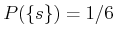
. The events include all subsets so that any probability
statement can be formulated. For example, what is the probability
that an even number is obtained? The event
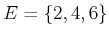
has
probability
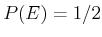
of occurring.

The third probability axiom looks similar to the last axiom in the
definition of a measure space in Section 5.1.3. In fact,
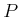 is technically a special kind of measure space as mentioned in
Example 5.12. If
is technically a special kind of measure space as mentioned in
Example 5.12. If 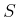 is continuous, however, this
measure cannot be captured by defining probabilities over the
singleton sets. The probabilities of singleton sets are usually zero.
Instead, a probability density function,
is continuous, however, this
measure cannot be captured by defining probabilities over the
singleton sets. The probabilities of singleton sets are usually zero.
Instead, a probability density function,
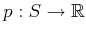 ,
is used to define the probability measure. The probability function,
,
is used to define the probability measure. The probability function,
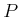 , for any event
, for any event
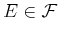 can then be determined via
integration:
can then be determined via
integration:
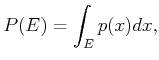 |
(9.3) |
in which 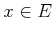 is the variable of integration. Intuitively,
is the variable of integration. Intuitively, 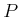 indicates the total probability mass that accumulates over
indicates the total probability mass that accumulates over 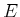 .
.
Steven M LaValle
2012-04-20

![]() , in which
the three components are
, in which
the three components are
![]() is technically a special kind of measure space as mentioned in
Example 5.12. If
is technically a special kind of measure space as mentioned in
Example 5.12. If ![]() is continuous, however, this
measure cannot be captured by defining probabilities over the
singleton sets. The probabilities of singleton sets are usually zero.
Instead, a probability density function,
is continuous, however, this
measure cannot be captured by defining probabilities over the
singleton sets. The probabilities of singleton sets are usually zero.
Instead, a probability density function,
![]() ,
is used to define the probability measure. The probability function,
,
is used to define the probability measure. The probability function,
![]() , for any event
, for any event
![]() can then be determined via
integration:
can then be determined via
integration: