A conditional probability is expressed as 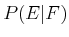 for any two
events
for any two
events
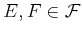 and is called the ``probability of
and is called the ``probability of 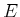 , given
, given
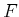 .'' Its definition is
.'' Its definition is
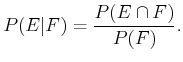 |
(9.4) |
Two events, 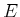 and
and 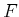 , are called independent if and only if
, are called independent if and only if
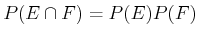 ; otherwise, they are called dependent. An important and sometimes misleading concept is
conditional independence. Consider some third event,
; otherwise, they are called dependent. An important and sometimes misleading concept is
conditional independence. Consider some third event,
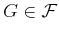 . It might be the case that
. It might be the case that 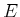 and
and 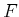 are dependent, but when
are dependent, but when
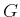 is given, they become independent. Thus,
is given, they become independent. Thus,
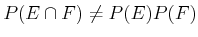 ; however,
; however,
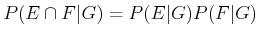 . Such examples
occur frequently in practice. For example,
. Such examples
occur frequently in practice. For example, 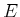 might indicate
someone's height, and
might indicate
someone's height, and 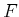 is their reading level. These will
generally be dependent events because children are generally shorter
and have a lower reading level. If we are given the person's age as
an event
is their reading level. These will
generally be dependent events because children are generally shorter
and have a lower reading level. If we are given the person's age as
an event 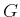 , then height is no longer important. It seems intuitive
that there should be no correlation between height and reading level
once the age is given.
, then height is no longer important. It seems intuitive
that there should be no correlation between height and reading level
once the age is given.
The definition of conditional probability, (9.4),
imposes the constraint that
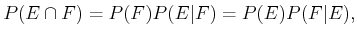 |
(9.5) |
which nicely relates 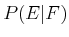 to
to 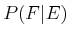 . This results in
Bayes' rule, which is a convenient way to swap
. This results in
Bayes' rule, which is a convenient way to swap 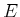 and
and 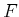 :
:
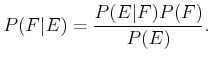 |
(9.6) |
The probability distribution, 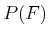 , is referred to as the prior, and
, is referred to as the prior, and 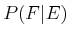 is the posterior.
These terms indicate that the probabilities come before and after
is the posterior.
These terms indicate that the probabilities come before and after 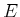 is considered, respectively.
is considered, respectively.
If all probabilities are conditioned on some event,
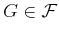 ,
then conditional Bayes' rule arises, which only differs from
(9.6) by placing the condition
,
then conditional Bayes' rule arises, which only differs from
(9.6) by placing the condition 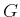 on all probabilities:
on all probabilities:
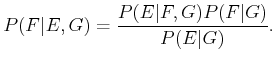 |
(9.7) |
Steven M LaValle
2012-04-20

![]() for any two
events
for any two
events
![]() and is called the ``probability of
and is called the ``probability of ![]() , given
, given
![]() .'' Its definition is
.'' Its definition is
![]() ,
then conditional Bayes' rule arises, which only differs from
(9.6) by placing the condition
,
then conditional Bayes' rule arises, which only differs from
(9.6) by placing the condition ![]() on all probabilities:
on all probabilities: