
Next: 9.2.4.2 Parameter estimation Up: 9.2.4.1 Pattern classification Previous: 9.2.4.1 Pattern classification
The probabilistic approach is most common in pattern classification.
This results in a Bayesian classifier. Here it is assumed that
![]() and
and ![]() are given. The distribution of features
for a given class is indicated by
are given. The distribution of features
for a given class is indicated by
![]() . The overall
frequency of class occurrences is given by
. The overall
frequency of class occurrences is given by ![]() . If large,
preclassified data sets are available, then these distributions can be
reliably learned. The feature space is often continuous, which
results in a density
. If large,
preclassified data sets are available, then these distributions can be
reliably learned. The feature space is often continuous, which
results in a density
![]() , even though
, even though ![]() remains a
discrete probability distribution. An optimal classifier,
remains a
discrete probability distribution. An optimal classifier, ![]() , is
designed according to (9.26). It performs classification
by receiving a feature vector,
, is
designed according to (9.26). It performs classification
by receiving a feature vector, ![]() , and then declaring that the class
is
, and then declaring that the class
is
![]() . The expected cost using (9.32) is
the probability of error.
. The expected cost using (9.32) is
the probability of error.
Suppose that there are three different image processing algorithms:
Imagine doing classification under the nondeterministic model, with
the assumption that the features always provide correct information.
For
![]() , the only possible letter is
, the only possible letter is ![]() . For
. For
![]() , the only letter is
, the only letter is ![]() . If each
. If each ![]() is consistent
with only one or no letters, then a perfect classifier can be
constructed. Unfortunately,
is consistent
with only one or no letters, then a perfect classifier can be
constructed. Unfortunately, ![]() is consistent with both
is consistent with both ![]() and
and
![]() . In the worst case, the cost of using (9.32) is
. In the worst case, the cost of using (9.32) is
![]() .
.
One way to fix this is to introduce a new feature. Suppose that an
image processing algorithm is used to detect corners. These are
places at which two segments meet at a right (![]() degrees) angle.
Let
degrees) angle.
Let ![]() denote the number of corners, and let the new feature
vector be
denote the number of corners, and let the new feature
vector be
![]() . The new algorithm nicely distinguishes
. The new algorithm nicely distinguishes
![]() from
from ![]() , for which
, for which ![]() and
and ![]() , respectively. Now all
letters can be correctly classified without errors.
, respectively. Now all
letters can be correctly classified without errors.
Of course, in practice, the image processing algorithms occasionally
make mistakes. A Bayesian classifier can be designed to maximize the
probability of success. Assume conditional independence of the
observations, which means that the classifier can be considered naive. Suppose that the four image
processing algorithms are run over a training data set and the
results are recorded. In each case, the correct classification is
determined by hand to obtain probabilities
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . For example, suppose
that the hole counter receives the letter
. For example, suppose
that the hole counter receives the letter ![]() as input. After running
the algorithm over many occurrences of
as input. After running
the algorithm over many occurrences of ![]() in text, it may be
determined that
in text, it may be
determined that
![]() , which is the correct
answer. With smaller probabilities, perhaps
, which is the correct
answer. With smaller probabilities, perhaps
![]() and
and
![]() . Assuming that the
output of each image processing algorithm is independent given the
input letter, a joint probability can be assigned as
. Assuming that the
output of each image processing algorithm is independent given the
input letter, a joint probability can be assigned as
| (9.33) |
The value of the prior ![]() can be obtained by running the
classifier over large amounts of hand-classified text and recording
the relative numbers of occurrences of each letter. It is interesting
to note that some context-specific information can be incorporated.
If the text is known to be written in Spanish, then
can be obtained by running the
classifier over large amounts of hand-classified text and recording
the relative numbers of occurrences of each letter. It is interesting
to note that some context-specific information can be incorporated.
If the text is known to be written in Spanish, then ![]() should
be different than from text written in English. Tailoring
should
be different than from text written in English. Tailoring ![]() to the type of text that will appear improves the performance of the
resulting classifier.
to the type of text that will appear improves the performance of the
resulting classifier.
The classifier makes its decisions by choosing the action that minimizes the probability of error. This error is proportional to
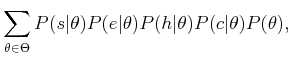 |
(9.34) |
Steven M LaValle 2012-04-20