
Next: Iterative deepening Up: 2.2.2 Particular Forward Search Previous: A-star
 |
For best-first search, the priority queue is sorted according to
an estimate of the optimal cost-to-go. The solutions obtained in this
way are not necessarily optimal; therefore, it does not matter whether
the estimate exceeds the true optimal cost-to-go, which was important
to maintain optimality for ![]() search. Although optimal solutions
are not found, in many cases, far fewer vertices are explored, which
results in much faster running times. There is no guarantee, however,
that this will happen. The worst-case performance of best-first
search is worse than that of
search. Although optimal solutions
are not found, in many cases, far fewer vertices are explored, which
results in much faster running times. There is no guarantee, however,
that this will happen. The worst-case performance of best-first
search is worse than that of ![]() search and dynamic programming.
The algorithm is often too greedy because it prefers states that
``look good'' very early in the search. Sometimes the price must be
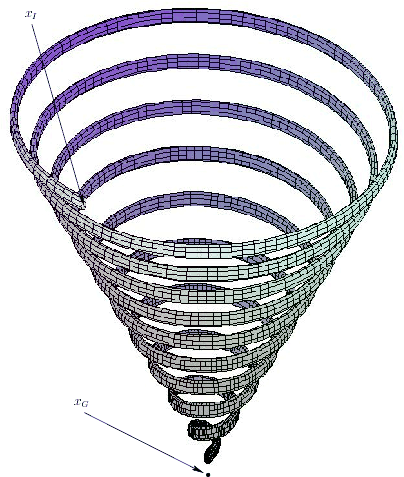
paid for being greedy! Figure 2.5 shows a contrived
example in which the planning problem involves taking small steps in a
3D world. For any specified number,
search and dynamic programming.
The algorithm is often too greedy because it prefers states that
``look good'' very early in the search. Sometimes the price must be
paid for being greedy! Figure 2.5 shows a contrived
example in which the planning problem involves taking small steps in a
3D world. For any specified number, ![]() , of steps, it is easy to
construct a spiral example that wastes at least
, of steps, it is easy to
construct a spiral example that wastes at least ![]() steps in
comparison to Dijkstra's algorithm. Note that best-first search is
not systematic.
steps in
comparison to Dijkstra's algorithm. Note that best-first search is
not systematic.
Steven M LaValle 2012-04-20