
Next: 2.3.2 Optimal Plans of Up: 2.3.1 Optimal Fixed-Length Plans Previous: 2.3.1.1 Backward value iteration
The ideas from Section 2.3.1 may be recycled to yield a
symmetrically equivalent method that computes optimal cost-to-come functions from the initial stage.
Whereas backward value iterations were able to find optimal plans from
all initial states simultaneously, forward value iterations can be
used to find optimal plans to all states in ![]() . In the backward
case,
. In the backward
case, ![]() must be fixed, and in the forward case,
must be fixed, and in the forward case, ![]() must
be fixed.
must
be fixed.
The issue of maintaining feasible solutions appears again. In the
forward direction, the role of ![]() is not important. It may be
applied in the last iteration, or it can be dropped altogether for
problems that do not have a predetermined
is not important. It may be
applied in the last iteration, or it can be dropped altogether for
problems that do not have a predetermined ![]() . However, one must
force all plans considered by forward value iteration to originate
from
. However, one must
force all plans considered by forward value iteration to originate
from ![]() . We again have the choice of either making notation
that imposes constraints on the action spaces or simply adding a term
that forces infeasible plans to have infinite cost. Once again, the
latter will be chosen here.
. We again have the choice of either making notation
that imposes constraints on the action spaces or simply adding a term
that forces infeasible plans to have infinite cost. Once again, the
latter will be chosen here.
Let ![]() denote the optimal cost-to-come from stage
denote the optimal cost-to-come from stage ![]() to
stage
to
stage ![]() , optimized over all
, optimized over all ![]() -step plans. To preclude plans
that do not start at
-step plans. To preclude plans
that do not start at ![]() , the definition of
, the definition of ![]() is given by
is given by
| (2.13) |
For an intermediate stage,
![]() , the following
represents the optimal cost-to-come:
, the following
represents the optimal cost-to-come:
As in (2.5), it is assumed in (2.14) that
![]() for every
for every
![]() . The resulting
. The resulting ![]() ,
obtained after applying
,
obtained after applying ![]() , must be the same
, must be the same ![]() that is named
in the argument on the left side of (2.14). It might appear
odd that
that is named
in the argument on the left side of (2.14). It might appear
odd that ![]() appears inside of the
appears inside of the ![]() above; however, this is
not a problem. The state
above; however, this is
not a problem. The state ![]() can be completely determined once
can be completely determined once
![]() and
and ![]() are given.
are given.
The final forward value iteration is the arrival at the final
stage, ![]() . The cost-to-come in this case is
. The cost-to-come in this case is
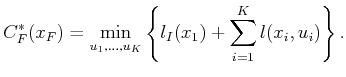 |
(2.15) |
To express the dynamic-programming recurrence, one further issue
remains. Suppose that ![]() is known by induction, and we
want to compute
is known by induction, and we
want to compute
![]() for a particular
for a particular ![]() . This means
that we must start at some state
. This means
that we must start at some state ![]() and arrive in state
and arrive in state ![]() by applying some action. Once again, the backward state transition
equation from Section
2.2.3 is useful. Using the stage indices, it is written here
as
by applying some action. Once again, the backward state transition
equation from Section
2.2.3 is useful. Using the stage indices, it is written here
as
![]() .
.
The recurrence is
Steven M LaValle 2012-04-20