
Next: 11.6.2 Sampling-Based Approaches Up: 11.6 Computing Probabilistic Information Previous: 11.6 Computing Probabilistic Information
This section covers the most successful and widely used example of a
derived I-space that dramatically collapses the history I-space. In
the special case in which both ![]() and
and ![]() are linear functions, and
are linear functions, and
![]() ,
, ![]() , and
, and ![]() are Gaussian, all probabilistic
I-states become Gaussian. This means that the probabilistic I-space,
are Gaussian, all probabilistic
I-states become Gaussian. This means that the probabilistic I-space,
![]() , does not need to represent every conceivable probability
density function. The probabilistic I-state is always trapped in the
subspace of
, does not need to represent every conceivable probability
density function. The probabilistic I-state is always trapped in the
subspace of
![]() that corresponds only to Gaussians. The
subspace is denoted as
that corresponds only to Gaussians. The
subspace is denoted as
![]() . This implies that an I-map,
. This implies that an I-map,
![]() , can be applied without
any loss of information.
, can be applied without
any loss of information.
The model is called linear-Gaussian (or LG). Each Gaussian density on
![]() is fully
specified by its
is fully
specified by its ![]() -dimensional mean vector
-dimensional mean vector ![]() and an
and an
![]() symmetric covariance matrix,
symmetric covariance matrix, ![]() . Therefore,
. Therefore,
![]() can
be considered as a subset of
can
be considered as a subset of
![]() in which
in which
![]() . For example, if
. For example, if
![]() , then
, then
![]() , because two independent parameters specify the mean
and three independent parameters specify the covariance matrix (not
four, because of symmetry). It was mentioned in Section
11.4.3 that moment-based approximations can be used in
general; however, for an LG model it is important to remember that
, because two independent parameters specify the mean
and three independent parameters specify the covariance matrix (not
four, because of symmetry). It was mentioned in Section
11.4.3 that moment-based approximations can be used in
general; however, for an LG model it is important to remember that
![]() is an exact representation of
is an exact representation of
![]() .
.
In addition to the fact that the
![]() collapses nicely,
collapses nicely,
![]() is a sufficient I-map, and convenient expressions exist
for incrementally updating the derived I-states entirely in terms of
the computed means and covariance. This implies that we can work
directly with
is a sufficient I-map, and convenient expressions exist
for incrementally updating the derived I-states entirely in terms of
the computed means and covariance. This implies that we can work
directly with
![]() , without any regard for the original
histories or even the general formulas for the probabilistic I-states
from Section 11.4.1. The update expressions are given here
without the full explanation, which is lengthy but not difficult and
can be found in virtually any textbook on stochastic control (e.g.,
[95,564]).
, without any regard for the original
histories or even the general formulas for the probabilistic I-states
from Section 11.4.1. The update expressions are given here
without the full explanation, which is lengthy but not difficult and
can be found in virtually any textbook on stochastic control (e.g.,
[95,564]).
For Kalman filtering, all of the required spaces are Euclidean, but
they may have different dimensions. Therefore, let
![]() ,
,
![]() , and
, and
![]() . Since Kalman filtering relies
on linear models, everything can be expressed in terms of matrix
transformations. Let
. Since Kalman filtering relies
on linear models, everything can be expressed in terms of matrix
transformations. Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() each
denote a matrix with constant real-valued entries and which may or
may not be singular. The dimensions of the matrices will be inferred
from the equations in which they will appear (the dimensions have to
be defined correctly to make the multiplications work out right). The
each
denote a matrix with constant real-valued entries and which may or
may not be singular. The dimensions of the matrices will be inferred
from the equations in which they will appear (the dimensions have to
be defined correctly to make the multiplications work out right). The
![]() subscript is used to indicate that a different matrix may be used
in each stage. In many applications, the matrices will be the same in
each stage, in which case they can be denoted by
subscript is used to indicate that a different matrix may be used
in each stage. In many applications, the matrices will be the same in
each stage, in which case they can be denoted by ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
and
,
and ![]() . Since Kalman filtering can handle the more general case, the
subscripts are included (even though they slightly complicate the
expressions).
. Since Kalman filtering can handle the more general case, the
subscripts are included (even though they slightly complicate the
expressions).
In general, the state transition equation,
![]() , is defined as
, is defined as
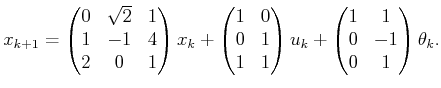 |
(11.76) |
The general form of the sensor mapping
![]() is
is
| (11.77) |
So far the linear part of the model has been given. The next step is
to specify the Gaussian part. In each stage, both nature actions
![]() and
and ![]() are modeled with zero-mean Gaussians. Thus,
each has an associated covariance matrix, denoted by
are modeled with zero-mean Gaussians. Thus,
each has an associated covariance matrix, denoted by
![]() and
and
![]() , respectively. Using the model given so far and
starting with an initial Gaussian density over
, respectively. Using the model given so far and
starting with an initial Gaussian density over ![]() , all resulting
probabilistic I-states will be Gaussian [564].
, all resulting
probabilistic I-states will be Gaussian [564].
Every derived I-state in
![]() can be represented by a mean and
covariance. Let
can be represented by a mean and
covariance. Let ![]() and
and ![]() denote the mean and covariance
of
denote the mean and covariance
of
![]() . The expressions given in the remainder of this
section define a derived information transition equation that computes
. The expressions given in the remainder of this
section define a derived information transition equation that computes
![]() and
and
![]() , given
, given ![]() ,
, ![]() ,
, ![]() , and
, and
![]() . The process starts by computing
. The process starts by computing ![]() and
and ![]() from the initial conditions.
from the initial conditions.
Assume that an initial condition is given that represents a Gaussian
density over
![]() . Let this be denoted by
. Let this be denoted by ![]() , and
, and ![]() .
The first I-state, which incorporates the first
observation
.
The first I-state, which incorporates the first
observation ![]() , is computed as
, is computed as
![]() and
and
| (11.78) |
| (11.79) |
Now that ![]() and
and ![]() have been expressed, the base case is
completed. The next part is to give the iterative updates from stage
have been expressed, the base case is
completed. The next part is to give the iterative updates from stage
![]() to stage
to stage ![]() . Using
. Using ![]() , the mean at the next stage is
computed as
, the mean at the next stage is
computed as
| (11.81) |
| (11.82) |
The most common use of the Kalman filter is to provide reliable
estimates of the state ![]() by using
by using ![]() . It turns out that
the optimal expected-cost feedback plan for a cost functional that is
a quadratic form can be obtained for LG systems in a closed-from
expression; see Section 15.2.2. This model is often called
LQG, to reflect the fact
that it is linear, quadratic-cost, and Gaussian. The optimal feedback
plan can even be expressed directly in terms of
. It turns out that
the optimal expected-cost feedback plan for a cost functional that is
a quadratic form can be obtained for LG systems in a closed-from
expression; see Section 15.2.2. This model is often called
LQG, to reflect the fact
that it is linear, quadratic-cost, and Gaussian. The optimal feedback
plan can even be expressed directly in terms of ![]() , without
requiring
, without
requiring ![]() . This indicates that the I-space may be
collapsed down to
. This indicates that the I-space may be
collapsed down to ![]() ; however, the corresponding I-map is not
sufficient. The covariances are still needed to compute the means, as
is evident from (11.80) and (11.83). Thus, an
optimal plan can be specified as
; however, the corresponding I-map is not
sufficient. The covariances are still needed to compute the means, as
is evident from (11.80) and (11.83). Thus, an
optimal plan can be specified as
![]() , but the
derived I-states in
, but the
derived I-states in
![]() need to be represented for the I-map
to be sufficient.
need to be represented for the I-map
to be sufficient.
The Kalman filter provides a beautiful solution to the class of linear Gaussian models. It is even successfully applied quite often in practice for problems that do not even satisfy these conditions. This is called the extended Kalman filter. The success may be explained by recalling that the probabilistic I-space may be approximated by mean and covariance in a second-order moment-based approximation. In general, such an approximation may be inappropriate, but it is nevertheless widely used in practice.
Steven M LaValle 2012-04-20