
Next: 2.4.2 Converting to the Up: 2.4 Using Logic to Previous: 2.4 Using Logic to
STRIPS-like representations have been the most common logic-based representations for discrete planning problems. This refers to the STRIPS system, which is considered one of the first planning algorithms and representations [337]; its name is derived from the STanford Research Institute Problem Solver. The original representation used first-order logic, which had great expressive power but many technical difficulties. Therefore, the representation was later restricted to only propositional logic [743], which is similar to the form introduced in this section. There are many variations of STRIPS-like representations. Here is one formulation:
Formulation 2.4.1 provides a definition of discrete
feasible planning expressed in a STRIPS-like
representation. The three most important components are the sets of
instances ![]() , predicates
, predicates ![]() , and operators
, and operators ![]() .
Informally, the instances characterize the complete set of distinct
things that exist in the world. They could, for example, be books,
cars, trees, and so on. The predicates correspond to basic properties or
statements that can be formed regarding the instances. For example, a
predicate called
.
Informally, the instances characterize the complete set of distinct
things that exist in the world. They could, for example, be books,
cars, trees, and so on. The predicates correspond to basic properties or
statements that can be formed regarding the instances. For example, a
predicate called ![]() might be used to indicate things like
might be used to indicate things like
![]() (the book is under the table) or
(the book is under the table) or
![]() . A predicate can be interpreted as a kind of
function that yields TRUE or FALSE values; however, it is important
to note that it is only a partial function because it might not be
desirable to allow any instance to be inserted as an argument to the
predicate.
. A predicate can be interpreted as a kind of
function that yields TRUE or FALSE values; however, it is important
to note that it is only a partial function because it might not be
desirable to allow any instance to be inserted as an argument to the
predicate.
If a predicate is evaluated on an instance, for example,
![]() , the expression is called a positive literal.
The set of all possible positive literals can be formed by applying
all possible instances to the domains over which the predicates are
defined. Every positive literal has a corresponding negative
literal, which is formed by negating the positive literal. For
example,
, the expression is called a positive literal.
The set of all possible positive literals can be formed by applying
all possible instances to the domains over which the predicates are
defined. Every positive literal has a corresponding negative
literal, which is formed by negating the positive literal. For
example,
![]() is the negative literal that
corresponds to the positive literal
is the negative literal that
corresponds to the positive literal
![]() , and
, and ![]() denotes negation. Let a complementary pair refer to a positive
literal together with its counterpart negative literal. The various
components of the planning problem are expressed in terms of positive
and negative literals.
denotes negation. Let a complementary pair refer to a positive
literal together with its counterpart negative literal. The various
components of the planning problem are expressed in terms of positive
and negative literals.
The role of an operator is to change the world. To be applicable, a set of preconditions must all be satisfied. Each element of this set is a positive or negative literal that must hold TRUE for the operator to be applicable. Any complementary pairs that can be formed from the predicates, but are not mentioned in the preconditions, may assume any value without affecting the applicability of the operator. If the operator is applied, then the world is updated in a manner precisely specified by the set of effects, which indicates positive and negative literals that result from the application of the operator. It is assumed that the truth values of all unmentioned complementary pairs are not affected.
Multiple operators are often defined in a single statement by using
variables. For example, ![]() may allow any instance
may allow any instance ![]() to be inserted. In some cases, this dramatically reduces the space
required to express the problem.
to be inserted. In some cases, this dramatically reduces the space
required to express the problem.
The planning problem is expressed in terms of an initial set ![]() of
positive literals and a goal set
of
positive literals and a goal set ![]() of positive and negative
literals. A state can be defined by selecting either the positive or
negative literal for every possible complementary pair. The initial
set
of positive and negative
literals. A state can be defined by selecting either the positive or
negative literal for every possible complementary pair. The initial
set ![]() specifies such a state by giving the positive literals only.
For all possible positive literals that do not appear in
specifies such a state by giving the positive literals only.
For all possible positive literals that do not appear in ![]() , it is
assumed that their negative counterparts hold in the initial state.
The goal set
, it is
assumed that their negative counterparts hold in the initial state.
The goal set ![]() actually refers to a set of states because, for any
unmentioned complementary pair, the positive or negative literal may
be chosen, and the goal is still achieved. The task is to find a
sequence of operators that when applied in succession will transform
the world from the initial state into one in which all literals of
actually refers to a set of states because, for any
unmentioned complementary pair, the positive or negative literal may
be chosen, and the goal is still achieved. The task is to find a
sequence of operators that when applied in succession will transform
the world from the initial state into one in which all literals of ![]() are TRUE. For each operator, the preconditions must also be
satisfied before it can be applied. The following example illustrates
Formulation 2.4.
are TRUE. For each operator, the preconditions must also be
satisfied before it can be applied. The following example illustrates
Formulation 2.4.
| (2.21) |
The initial set is
| (2.22) |
The goal state is
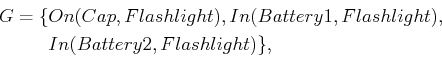 |
(2.23) |
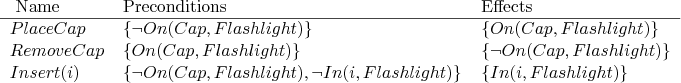 |
The set ![]() consists of the four operators, which are shown in Figure
2.18. Here is a plan that reaches the goal state in the
smallest number of steps:
consists of the four operators, which are shown in Figure
2.18. Here is a plan that reaches the goal state in the
smallest number of steps:
This example appears quite simple, and one would expect a planning
algorithm to easily find such a solution. It can be made more
challenging by adding many more instances to ![]() , such as more
batteries, more flashlights, and a bunch of objects that are
irrelevant to achieving the goal. Also, many other predicates and
operators can be added so that the different combinations of operators
become overwhelming.
, such as more
batteries, more flashlights, and a bunch of objects that are
irrelevant to achieving the goal. Also, many other predicates and
operators can be added so that the different combinations of operators
become overwhelming.
![]()
A large number of complexity results exist for planning expressed using logic. The graph search problem is solved efficiently in polynomial time; however, a state transition graph is not given as the input. An input that is expressed using Formulation 2.4 may describe an enormous state transition graph using very few instances, predicates, and operators. In a sense, the model is highly compressed when using some logic-based formulations. This brings it closer to the Kolmogorov complexity [248,630] of the state transition graph, which is the shortest bit size to which it can possibly be compressed and then fully recovered by a Turing machine. This has the effect of making the planning problem appear more difficult. Concise inputs may encode very challenging planning problems. Most of the known hardness results are surveyed in Chapter 3 of [382]. Under most formulations, logic-based planning is NP-hard. The particular level of hardness (NP, PSPACE, EXPTIME, etc.) depends on the precise problem conditions. For example, the complexity depends on whether the operators are fixed in advance or included in the input. The latter case is much harder. Separate complexities are also obtained based on whether negative literals are allowed in the operator effects and also whether they are allowed in preconditions. The problem is generally harder if both positive and negative literals are allowed in these cases.
Steven M LaValle 2012-04-20