
Next: 12.3 Environment Uncertainty and Up: 12.2.3 Probabilistic Methods for Previous: Discrete problems
 |
Localization in a continuous space using probabilistic models has
received substantial attention in recent years
[258,447,622,825,887,962].
It is often difficult to localize mobile robots because of noisy
sensor data, modeling errors, and high demands for robust operation
over long time periods. Probabilistic modeling and the computation of
probabilistic I-states have been quite successful in many experimental
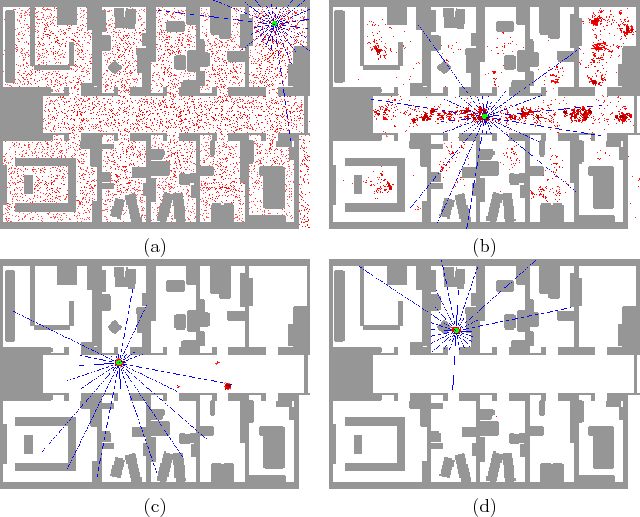
systems, both for indoor and outdoor mobile robots. Figure
12.11 shows localization successfully being solved using
sonars only. The vast majority of work in this context involves
passive localization because the robot is often completing some other
task, such as reaching a particular part of the environment.
Therefore, the focus is mainly on computing the probabilistic
I-states, rather than performing a difficult search on
![]() .
.
Probabilistic localization in continuous spaces most often involves
the definition of the probability densities
![]() and
and
![]() (in the case of a state sensor mapping). If the stages
represent equally spaced times, then these densities usually remain
fixed for every stage. The state space is usually
(in the case of a state sensor mapping). If the stages
represent equally spaced times, then these densities usually remain
fixed for every stage. The state space is usually ![]() to
account for translation and rotation, but it may be
to
account for translation and rotation, but it may be
![]() for
translation only. The density
for
translation only. The density
![]() accounts for the
unpredictability that arises when controlling a mobile robot over some
fixed time interval. A method for estimating this distribution for
nonholonomic robots by solving stochastic differential equations
appears in [1004].
accounts for the
unpredictability that arises when controlling a mobile robot over some
fixed time interval. A method for estimating this distribution for
nonholonomic robots by solving stochastic differential equations
appears in [1004].
The density
![]() indicates the relative likelihood of various
measurements when given the state. Most often this models distance
measurements that are obtained from a laser range scanner, an array of
sonars, or even infrared sensors. Suppose that a robot moves around
in a 2D environment and takes depth measurements at various
orientations. In the robot body frame, there are
indicates the relative likelihood of various
measurements when given the state. Most often this models distance
measurements that are obtained from a laser range scanner, an array of
sonars, or even infrared sensors. Suppose that a robot moves around
in a 2D environment and takes depth measurements at various
orientations. In the robot body frame, there are ![]() angles at which
a depth measurement is taken. Ideally, the measurements should look
like those in Figure 11.15b; however, in practice, the data
contain substantial noise. The observation
angles at which
a depth measurement is taken. Ideally, the measurements should look
like those in Figure 11.15b; however, in practice, the data
contain substantial noise. The observation ![]() is an
is an
![]() -dimensional vector of noisy depth measurements.
-dimensional vector of noisy depth measurements.
One common way to define ![]() is to assume that the error in each
distance measurement follows a Gaussian density. The mean value of
the measurement can easily be calculated as the true distance value
once
is to assume that the error in each
distance measurement follows a Gaussian density. The mean value of
the measurement can easily be calculated as the true distance value
once ![]() is given, and the variance should be determined from
experimental evaluation of the sensor. If it is assumed that the
vector of measurements is modeled as a set of independent, identically
distributed random variables, a simple product of Guassian densities is
obtained for
is given, and the variance should be determined from
experimental evaluation of the sensor. If it is assumed that the
vector of measurements is modeled as a set of independent, identically
distributed random variables, a simple product of Guassian densities is
obtained for ![]() .
.
Once the models have been formulated, the computation of probabilistic
I-states directly follows from Sections 11.2.3 and
11.4.1. The initial condition is a probability density
function, ![]() , over
, over ![]() . The marginalization and Bayesian update
rules are then applied to construct a sequence of density functions of
the form
. The marginalization and Bayesian update
rules are then applied to construct a sequence of density functions of
the form
![]() for every stage,
for every stage, ![]() .
.
In some limited applications, the models used to express
![]() and
and
![]() may be linear and Gaussian. In
this case, the Kalman filter of Section 11.6.1 can be easily
applied. In most cases, however, the densities will not have this
form. Moment-based approximations, as discussed in Section
11.4.3, can be used to approximate the densities. If
second-order moments are used, then the so-called extended Kalman
filter is obtained, in which the Kalman filter update rules can be
applied to a linear-Gaussian
approximation to the original problem. In recent years, one of the
most widely accepted approaches in experimental mobile robotics is to
use sampling-based techniques to directly compute and estimate the
probabilistic I-states. The particle-filtering approach, described in
general in Section 11.6.2, appears to provide good
experimental performance when applied to localization. The
application of particle filtering in this context is often
referred to as Monte Carlo localization; see the references at
the end of this chapter.
may be linear and Gaussian. In
this case, the Kalman filter of Section 11.6.1 can be easily
applied. In most cases, however, the densities will not have this
form. Moment-based approximations, as discussed in Section
11.4.3, can be used to approximate the densities. If
second-order moments are used, then the so-called extended Kalman
filter is obtained, in which the Kalman filter update rules can be
applied to a linear-Gaussian
approximation to the original problem. In recent years, one of the
most widely accepted approaches in experimental mobile robotics is to
use sampling-based techniques to directly compute and estimate the
probabilistic I-states. The particle-filtering approach, described in
general in Section 11.6.2, appears to provide good
experimental performance when applied to localization. The
application of particle filtering in this context is often
referred to as Monte Carlo localization; see the references at
the end of this chapter.
Steven M LaValle 2012-04-20