
Next: Algorithms for determining the Up: 12.3 Environment Uncertainty and Previous: 12.3 Environment Uncertainty and
To gain a clear understanding of the issues, it will once again be
helpful to consider discrete problems. The discussion here is a
continuation of Section 12.2.1. In that section, the state
represented a position, ![]() , and a direction,
, and a direction, ![]() . Now suppose that
the state is represented as
. Now suppose that
the state is represented as ![]() , in which
, in which ![]() represents the
particular environment that contains the robot. This will require
defining a space of environments, which is rarely represented
explicitly. It is often expressed as a constraint on the types of
environments that can exist. For example, the set of environments
could be defined as all connected 2D grid-planning problems. The set
of simply connected grid-planning problems is even further
constrained.
represents the
particular environment that contains the robot. This will require
defining a space of environments, which is rarely represented
explicitly. It is often expressed as a constraint on the types of
environments that can exist. For example, the set of environments
could be defined as all connected 2D grid-planning problems. The set
of simply connected grid-planning problems is even further
constrained.
One question immediately arises: When are two maps of an environment
equivalent? Recall the maps shown in Figures 12.2a and
12.3b. The map in Figure 12.3b appears the
same for every 90-degree rotation; however, the map in Figure
12.2a appears to be different. Even if it appears
different, it should still be the same environment, right? Imagine
mapping a remote island without having a compass that indicates the
direction to the north pole. An orientation (which way is up?) for
the map can be chosen arbitrarily without any harm. If a map of the
environment is made by ``drawing'' on
![]() , it should seem that two
maps are equivalent if a transformation in
, it should seem that two
maps are equivalent if a transformation in ![]() (i.e., translation
and rotation) can be applied to overlay one perfectly on top of the
other.
(i.e., translation
and rotation) can be applied to overlay one perfectly on top of the
other.
When defining an environment space, it is important to clearly define
what it means for two environments to be equivalent. For example, if
we are required to build a map by exploration, is it required to also
provide the exact translation and orientation? This may or may not be
required, but it is important to specify this in the problem
description. Thus, we will allow any possibility: If the maps only
differ by a transformation in ![]() , they may or may not be defined
as equivalent, depending on the application.
, they may or may not be defined
as equivalent, depending on the application.
To consider some examples, it will be convenient to define some finite
or infinite sets of environments. Suppose that planning on a 2D grid
is once again considered. In this section, assume that each grid
point ![]() has integer coordinates
has integer coordinates
![]() , as
defined in Section 2.1. Let
, as
defined in Section 2.1. Let ![]() denote a set of
environments. Once again, there are four possible directions for the
robot to face; let
denote a set of
environments. Once again, there are four possible directions for the
robot to face; let ![]() denote this set. The state space is
denote this set. The state space is
Examples will be given shortly, but first think about the kinds of problems that can be formulated:
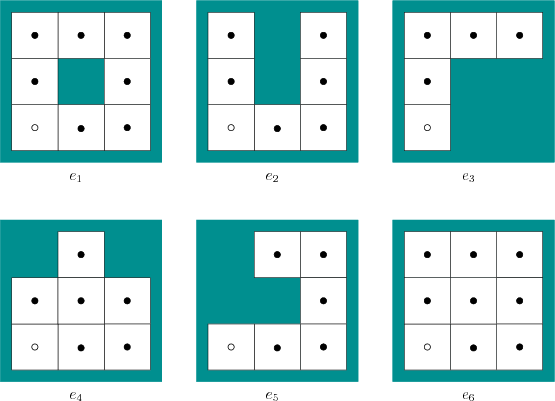 |
 |
The initial condition is ![]() , because any position, orientation, and
environment are possible. Some nondeterministic I-states will now be
determined. Let
, because any position, orientation, and
environment are possible. Some nondeterministic I-states will now be
determined. Let
![]() . From
this sequence of actions, the sensor observations
. From
this sequence of actions, the sensor observations
![]() report that the robot has not yet changed its position. The
orientation was changed to west, but this is not known to the robot
(it does, however, know that it is now pointing in the opposite
direction with respect to its initial orientation). What can now be
inferred? The robot has discovered that it is on a tile that is
bounded on three sides by obstacles. This means that
report that the robot has not yet changed its position. The
orientation was changed to west, but this is not known to the robot
(it does, however, know that it is now pointing in the opposite
direction with respect to its initial orientation). What can now be
inferred? The robot has discovered that it is on a tile that is
bounded on three sides by obstacles. This means that ![]() and
and ![]() are ruled out as possible environments. In the remaining four
environments, the robot deduces that it must be on one of the end
tiles: 1) the upper left of
are ruled out as possible environments. In the remaining four
environments, the robot deduces that it must be on one of the end
tiles: 1) the upper left of ![]() , 2) the upper right of
, 2) the upper right of ![]() , 3) the
bottom of
, 3) the
bottom of ![]() , 4) the rightmost of
, 4) the rightmost of ![]() , 5) the top of
, 5) the top of ![]() , 6)
the lower left of
, 6)
the lower left of ![]() , or 7) the upper left of
, or 7) the upper left of ![]() . It can also
make strong inferences regarding its orientation. It even knows that
the action
. It can also
make strong inferences regarding its orientation. It even knows that
the action
![]() would cause it to move because all four
directions cannot be blocked.
would cause it to move because all four
directions cannot be blocked.
Apply
![]() . The robot should move two
times, to arrive in the upper left of
. The robot should move two
times, to arrive in the upper left of ![]() facing north. In this
case, any of
facing north. In this
case, any of ![]() ,
, ![]() ,
, ![]() , or
, or ![]() are still possible;
however, it now knows that its position at stage
are still possible;
however, it now knows that its position at stage ![]() could not have
been in the upper left of
could not have
been in the upper left of ![]() . If the robot is in
. If the robot is in ![]() , it knows
that it must be in the upper left, but it still does not know its
orientation (it could be north or west). The robot could also be in
the lower left or lower right of
, it knows
that it must be in the upper left, but it still does not know its
orientation (it could be north or west). The robot could also be in
the lower left or lower right of ![]() .
.
Now let
![]() , which moves the robot
twice. At this point,
, which moves the robot
twice. At this point, ![]() and
and ![]() are ruled out, and the set of
possible environments is
are ruled out, and the set of
possible environments is
![]() (one orientation from
(one orientation from ![]() is
also ruled out). If
is
also ruled out). If
![]() is applied, then the sensor
observation
is applied, then the sensor
observation ![]() reports that the robot does not move. This rules
out
reports that the robot does not move. This rules
out ![]() . Finally, the robot can deduce that it is in the upper
right of
. Finally, the robot can deduce that it is in the upper
right of ![]() facing south. It can also deduce that in its initial
state it was in the lower left of
facing south. It can also deduce that in its initial
state it was in the lower left of ![]() facing east. Thus, all of the
uncertainty has been eliminated through the construction of the
nondeterministic I-states.
facing east. Thus, all of the
uncertainty has been eliminated through the construction of the
nondeterministic I-states.
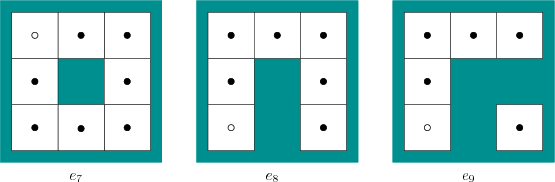
Now consider adding the environments shown in Figure 12.13
to the set and starting the problem over again. Environment ![]() is
identical to
is
identical to ![]() , except that the origin is moved, and
, except that the origin is moved, and ![]() is
identical to
is
identical to ![]() , except that it is rotated by
, except that it is rotated by ![]() degrees. In
these two cases, there exist no inputs that enable the robot to
distinguish between
degrees. In
these two cases, there exist no inputs that enable the robot to
distinguish between ![]() and
and ![]() or between
or between ![]() and
and ![]() . It
is reasonable to declare these environments to be pairwise equivalent.
The only distinction between them is the way that the map is drawn.
. It
is reasonable to declare these environments to be pairwise equivalent.
The only distinction between them is the way that the map is drawn.
If the robot executes the same action sequence as given previously,
then it will also not be able to distinguish ![]() from
from ![]() . It is
impossible for the robot to deduce whether there is a white tile
somewhere that is not reachable. A general environment space may
include such variations, and this will prevent the robot from knowing
the precise environment. However, this usually presents no additional
difficulty in solving a planning problem. Therefore, it might make
sense to declare
. It is
impossible for the robot to deduce whether there is a white tile
somewhere that is not reachable. A general environment space may
include such variations, and this will prevent the robot from knowing
the precise environment. However, this usually presents no additional
difficulty in solving a planning problem. Therefore, it might make
sense to declare ![]() and
and ![]() to be equivalent. The fact that
tasks can be achieved without knowing the precise environment is very
important. In a sense, the environment is observed at some
``resolution'' that is sufficient for solving a problem; further
details beyond that are unimportant. Since the robot can ignore
unnecessary details, cheaper and more reliable systems can often be
built.
to be equivalent. The fact that
tasks can be achieved without knowing the precise environment is very
important. In a sense, the environment is observed at some
``resolution'' that is sufficient for solving a problem; further
details beyond that are unimportant. Since the robot can ignore
unnecessary details, cheaper and more reliable systems can often be
built.
![]()