For purposes of illustration, suppose that
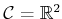 . A
configuration is expressed as
. A
configuration is expressed as
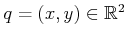 , and a velocity is
expressed as
, and a velocity is
expressed as
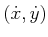 . Each
. Each
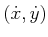 is an element of
the tangent space
is an element of
the tangent space
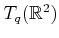 , which is a two-dimensional vector
space at every
, which is a two-dimensional vector
space at every 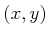 . Think about the kinds of constraints that
could be imposed. At each
. Think about the kinds of constraints that
could be imposed. At each
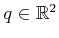 , restricting the set of
velocities yields some set
, restricting the set of
velocities yields some set
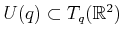 . The parametric
and implicit representations will be alternative ways to express
. The parametric
and implicit representations will be alternative ways to express
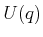 for all
for all
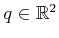 .
.
Here are some interesting, simple constraints. Each yields a
definition of 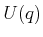 as the subset of
as the subset of
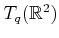 that satisfies the
constraints.
that satisfies the
constraints.
-
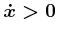 : In this case, imagine that you are
paddling a boat on a swift river that flows in the positive
: In this case, imagine that you are
paddling a boat on a swift river that flows in the positive  direction. You can obtain any velocity you like in the
direction. You can obtain any velocity you like in the 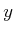 direction,
but you can never flow against the current. This means that all
integral curves increase monotonically in
direction,
but you can never flow against the current. This means that all
integral curves increase monotonically in  over time.
over time.
-
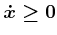 : This constraint allows you to
stop moving in the
: This constraint allows you to
stop moving in the  direction. A velocity perpendicular to the
current can be obtained (for example,
direction. A velocity perpendicular to the
current can be obtained (for example, 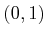 causes motion with unit
speed in the positive
causes motion with unit
speed in the positive 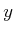 direction).
direction).
-
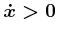 ,
,
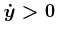 : Under this constraint, integral
curves must monotonically increase in both
: Under this constraint, integral
curves must monotonically increase in both  and
and 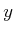 .
.
-
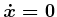 : In the previous three examples,
the set of allowable velocities remained two-dimensional. Under the
constraint
: In the previous three examples,
the set of allowable velocities remained two-dimensional. Under the
constraint
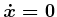 , the set of allowable velocities is only
one-dimensional. All vectors of the form
, the set of allowable velocities is only
one-dimensional. All vectors of the form
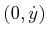 for any
for any
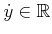 are allowed. This means that no motion in the
are allowed. This means that no motion in the  direction
is allowed. Starting at any
direction
is allowed. Starting at any 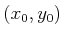 , the integral curves will be
of the form
, the integral curves will be
of the form
 for all
for all
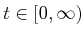 , which confines
each one to a vertical line.
, which confines
each one to a vertical line.
-
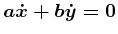 : This constraint is qualitatively the
same as the previous one. The difference is that now the motions can
be restricted along any collection of parallel lines by choosing
: This constraint is qualitatively the
same as the previous one. The difference is that now the motions can
be restricted along any collection of parallel lines by choosing 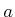 and
and 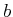 . For example, if
. For example, if 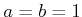 , then only diagonal motions are
allowed.
, then only diagonal motions are
allowed.
-
 : This constraint is
similar to the previous one, however the behavior is quite different
because the integral curves do not coincide. An entire half plane
is reached. It also impossible to stop becasue
: This constraint is
similar to the previous one, however the behavior is quite different
because the integral curves do not coincide. An entire half plane
is reached. It also impossible to stop becasue
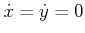 violates the constraint.
violates the constraint.
-
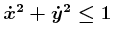 : This constraint was
used in Chapter 8. It has no effect on the existence
of solutions to the feasible motion planning problem because motion in
any direction is still allowed. The constraint only enforces a
maximum speed.
: This constraint was
used in Chapter 8. It has no effect on the existence
of solutions to the feasible motion planning problem because motion in
any direction is still allowed. The constraint only enforces a
maximum speed.
-
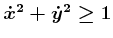 : This constraint
allows motions in any direction and at any speed greater than
: This constraint
allows motions in any direction and at any speed greater than 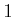 . It
is impossible to stop or slow down below unit speed.
. It
is impossible to stop or slow down below unit speed.
Many other constraints can be imagined, including some that define
very complicated regions in
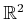 for each
for each 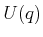 . Ignoring the
fact that
. Ignoring the
fact that 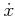 and
and 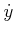 represent derivatives, the geometric
modeling concepts from Section 3.1 can even be used to define
complicated constraints at each
represent derivatives, the geometric
modeling concepts from Section 3.1 can even be used to define
complicated constraints at each 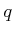 . In fact, the constraints
expressed above in terms of
. In fact, the constraints
expressed above in terms of 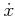 and
and 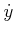 are simple examples of
the semi-algebraic model, which was introduced in Section
3.1.2. Just replace
are simple examples of
the semi-algebraic model, which was introduced in Section
3.1.2. Just replace  and
and 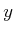 from that section
by
from that section
by 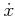 and
and 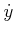 here.
here.
If at every 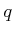 there exists some open set
there exists some open set 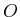 such that
such that
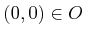 and
and
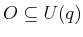 , then there is no effect on the existence of
solutions to the feasible motion planning problem. Velocities in all
directions are still allowed. This holds true for velocity
constraints on any smooth manifold [924].
, then there is no effect on the existence of
solutions to the feasible motion planning problem. Velocities in all
directions are still allowed. This holds true for velocity
constraints on any smooth manifold [924].
So far, the velocities have been constrained in the same way at every
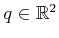 , which means that
, which means that 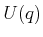 is the same for all
is the same for all
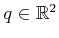 . Constraints of this kind are of the form
. Constraints of this kind are of the form
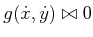 , in which
, in which 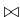 could be
could be 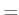 ,
, 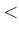 ,
, 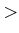 ,
, 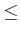 , or
, or
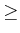 , and
, and 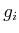 is a function from
is a function from
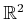 to
to
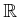 . Typically, the
. Typically, the
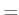 relation drops the dimension of
relation drops the dimension of 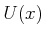 by one, and the others
usually leave it unchanged.
by one, and the others
usually leave it unchanged.
Now consider the constraint
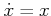 . This results in a different
one-dimensional set,
. This results in a different
one-dimensional set, 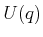 , of allowable velocities at each
, of allowable velocities at each
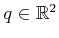 . At each
. At each 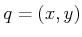 , the set of allowable velocities must be
of the form
, the set of allowable velocities must be
of the form
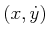 for any
for any
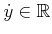 . This means that as
. This means that as
 increases, the velocity in the
increases, the velocity in the  direction must increase
proportionally. Starting at any positive
direction must increase
proportionally. Starting at any positive  value, there is no way
to travel to the
value, there is no way
to travel to the 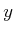 -axis. However, starting on the
-axis. However, starting on the 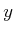 -axis, the
integral curves will always remain on it! Constraints of this kind
can generally be expressed as
-axis, the
integral curves will always remain on it! Constraints of this kind
can generally be expressed as
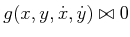 , which
allows the dependency on
, which
allows the dependency on  or
or 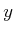 .
.
Steven M LaValle
2012-04-20

![]() . A
configuration is expressed as
. A
configuration is expressed as
![]() , and a velocity is
expressed as
, and a velocity is
expressed as
![]() . Each
. Each
![]() is an element of
the tangent space
is an element of
the tangent space
![]() , which is a two-dimensional vector
space at every
, which is a two-dimensional vector
space at every ![]() . Think about the kinds of constraints that
could be imposed. At each
. Think about the kinds of constraints that
could be imposed. At each
![]() , restricting the set of
velocities yields some set
, restricting the set of
velocities yields some set
![]() . The parametric
and implicit representations will be alternative ways to express
. The parametric
and implicit representations will be alternative ways to express
![]() for all
for all
![]() .
.
![]() as the subset of
as the subset of
![]() that satisfies the
constraints.
that satisfies the
constraints.
![]() there exists some open set
there exists some open set ![]() such that
such that
![]() and
and
![]() , then there is no effect on the existence of
solutions to the feasible motion planning problem. Velocities in all
directions are still allowed. This holds true for velocity
constraints on any smooth manifold [924].
, then there is no effect on the existence of
solutions to the feasible motion planning problem. Velocities in all
directions are still allowed. This holds true for velocity
constraints on any smooth manifold [924].
![]() , which means that
, which means that ![]() is the same for all
is the same for all
![]() . Constraints of this kind are of the form
. Constraints of this kind are of the form
![]() , in which
, in which ![]() could be
could be ![]() ,
, ![]() ,
, ![]() ,
, ![]() , or
, or
![]() , and
, and ![]() is a function from
is a function from
![]() to
to
![]() . Typically, the
. Typically, the
![]() relation drops the dimension of
relation drops the dimension of ![]() by one, and the others
usually leave it unchanged.
by one, and the others
usually leave it unchanged.
![]() . This results in a different
one-dimensional set,
. This results in a different
one-dimensional set, ![]() , of allowable velocities at each
, of allowable velocities at each
![]() . At each
. At each ![]() , the set of allowable velocities must be
of the form
, the set of allowable velocities must be
of the form
![]() for any
for any
![]() . This means that as
. This means that as
![]() increases, the velocity in the
increases, the velocity in the ![]() direction must increase
proportionally. Starting at any positive
direction must increase
proportionally. Starting at any positive ![]() value, there is no way
to travel to the
value, there is no way
to travel to the ![]() -axis. However, starting on the
-axis. However, starting on the ![]() -axis, the
integral curves will always remain on it! Constraints of this kind
can generally be expressed as
-axis, the
integral curves will always remain on it! Constraints of this kind
can generally be expressed as
![]() , which
allows the dependency on
, which
allows the dependency on ![]() or
or ![]() .
.