
Next: 13.3.3 Motion of a Up: 13.3.2 Motions of Particles Previous: 13.3.2.1 Motion of a
The concepts expressed so far naturally extend to a set of particles that move in a closed system. This provides a smooth transition to rigid bodies, which are modeled as a collection of infinitesimal particles that are ``stuck together,'' causing forces between neighboring particles to cancel. In the present model, the particles are independently moving. If a pair of particles collides, then, by Newton's third law, they receive forces of equal magnitude and opposite directions at the instant of impact.
It can be shown that all momentum expressions extend to sums over the particles [681]. For a set of particles, the linear momentum of each can be summed to yield the linear momentum of the system as
| (13.71) |
| (13.72) |
| (13.73) |
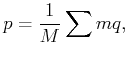 |
(13.74) |
So far the translational part of the motion has been captured; however, rotation of the system is also important. This was the motivation for introducing the moment concepts. Let the total moment of force (or total torque) be
| (13.75) |
| (13.76) |
The ideas given so far make a system of particles appear very much as a single particle. It is important, however, when conducting a simulation of their behavior to consider the collisions between the particles. Detecting these collisions and calculating the resulting impact forces ensures that correct motions are obtained.
As the number of particles tends to infinity, consider the limiting case of a rigid body. In this case, the particles are ``sewn'' together, which cancels their internal forces. It will be sufficient only to handle the forces that act on the boundary of the rigid body. The expressions for the motion of a rigid body are given in Section 13.3.3. The expressions can alternatively be obtained using other concepts, such as those in Section 13.4.
Steven M LaValle 2012-04-20