
Next: 13.4.3 Extensions of the Up: 13.4.2 General Lagrangian Expressions Previous: 13.4.2 General Lagrangian Expressions
The final step is to convert the equations into phase space form. A
![]() -dimensional phase vector is introduced as
-dimensional phase vector is introduced as
![]() . The
task is to obtain
. The
task is to obtain
![]() , which represents
, which represents ![]() scalar
equations. The first
scalar
equations. The first ![]() equations are
equations are
![]() for
for ![]() from
from ![]() to
to ![]() . The final
. The final ![]() equations are obtained by solving for
equations are obtained by solving for
![]() .
.
Suppose that the general form in (13.142) is used. Solving
for ![]() yields
yields
Rather than performing the computations directly using (13.118), the constraints can be directly determined using (13.140). The terms are
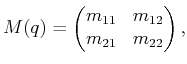 |
(13.155) |
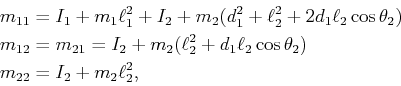 |
(13.156) |
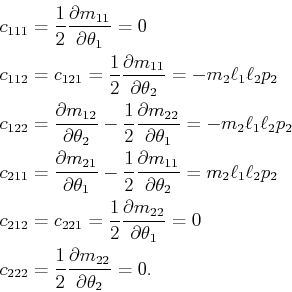 |
(13.157) |
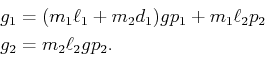 |
(13.158) |
The dynamics can alternatively be expressed using ![]() ,
,
![]() , and
, and ![]() in (13.142). The Coriolis
matrix is defined using (13.143) to obtain
in (13.142). The Coriolis
matrix is defined using (13.143) to obtain
The phase transition equation is obtained by letting
![]() and substituting the
state variables into (13.161). The variables
and substituting the
state variables into (13.161). The variables
![]() and
and
![]() become
become
![]() and
and
![]() ,
respectively. The equations must be solved for
,
respectively. The equations must be solved for
![]() and
and
![]() .
An extension of this model to motors that have gear ratios and
nonnegligible mass appears in [856].
.
An extension of this model to motors that have gear ratios and
nonnegligible mass appears in [856].
![]()
The example provided here barely scratches the surface on the possible systems that can be elegantly modeled. Many robotics texts cover cases in which there are more links, different kinds of joints, and frictional forces [366,725,856,907,994].
The phase transition equation for chains of bodies could alternatively be derived using the Newton-Euler formulation of mechanics. Even though the Lagrangian form is more elegant, the Newton-Euler equations, when expressed recursively, are far more efficient for simulations of multibody dynamical systems [366,863,994].
Steven M LaValle 2012-04-20