
Next: 14.1.3.1 Additional constraints on Up: 14.1 Introduction Previous: Symmetric systems
In Formulation 14.1, the specification of the obstacle
region in Item 4 was intentionally left ambiguous. Now
it will be specified in more detail. If
![]() , then
, then
![]() , which was defined in (4.34) for a rigid robot and in
(4.36) for a robot with multiple links. The more
interesting case occurs if
, which was defined in (4.34) for a rigid robot and in
(4.36) for a robot with multiple links. The more
interesting case occurs if ![]() is a phase space that includes velocity
variables in addition to configuration information.
is a phase space that includes velocity
variables in addition to configuration information.
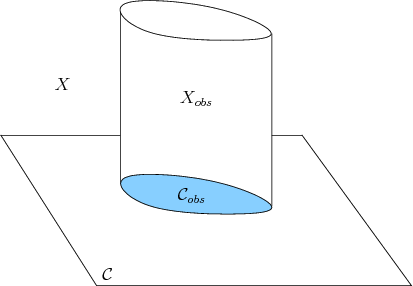 |
Any state for which its associated configuration lies in
![]() must
also be a member of
must
also be a member of ![]() . The velocity is irrelevant if a
collision occurs in the world
. The velocity is irrelevant if a
collision occurs in the world ![]() . In most cases that involve a
phase space, the obstacle region
. In most cases that involve a
phase space, the obstacle region ![]() is therefore defined as
is therefore defined as