
Next: 14.2.2.1 Reachability graph Up: 14.2 Reachability and Completeness Previous: 14.2.1.3 Backward reachable sets
This section introduces a simple and effective way to sample the space
of action trajectories. Section 14.2.3 covers the more
general case. Under differential constraints, sampling-based motion
planning algorithms all work by sampling the space of action
trajectories. This results in a reduced set of possible action
trajectories. To ensure some form of completeness, a motion planning
algorithm should carefully construct and refine the sample set. As in
Chapter 5, the qualities of a sample set can be
expressed in terms of dispersion and denseness. The main difference
in the current setting is that the algorithms here work with a sample
sequence over ![]() , as opposed to over
, as opposed to over ![]() as in Chapter
5. This is required because solution paths can no
longer be expressed directly on
as in Chapter
5. This is required because solution paths can no
longer be expressed directly on ![]() (or
(or ![]() ).
).
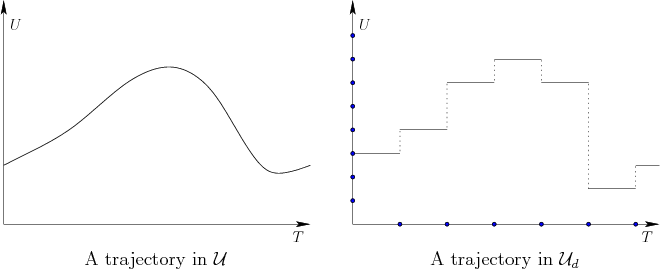 |
The discrete-time model is depicted in Figure 14.5 and is characterized by three aspects:
For some problems, ![]() may already be finite. Imagine, for example, a
model of firing one of several thrusters (turn them on or off) on a free-floating spacecraft. In this case no discretization
of
may already be finite. Imagine, for example, a
model of firing one of several thrusters (turn them on or off) on a free-floating spacecraft. In this case no discretization
of ![]() is necessary. In the more general case,
is necessary. In the more general case, ![]() may be a
continuous set. The sampling methods of Section 5.2 can
be applied to determine a finite subset
may be a
continuous set. The sampling methods of Section 5.2 can
be applied to determine a finite subset
![]() .
.
Any action trajectory in
![]() can be conveniently expressed as an
action sequence
can be conveniently expressed as an
action sequence
![]() , in which each
, in which each
![]() gives the action to apply from time
gives the action to apply from time
![]() to time
to time
![]() . After stage
. After stage ![]() , it is assumed that the termination action
is applied.
, it is assumed that the termination action
is applied.