
Next: 14.2.2.2 Resolution completeness for Up: 14.2.2 The Discrete-Time Model Previous: 14.2.2 The Discrete-Time Model
After time discretization has been performed, the reachable set can be
adapted to
![]() to obtain
to obtain
![]() . An interesting question
is: What is the effect of sampling on the reachable set? In other
words, how do
. An interesting question
is: What is the effect of sampling on the reachable set? In other
words, how do
![]() and
and
![]() differ? This can be
addressed by defining a reachability graph, which will be revealed
incrementally by a planning algorithm.
differ? This can be
addressed by defining a reachability graph, which will be revealed
incrementally by a planning algorithm.
Let
![]() denote a reachability tree, which encodes
the set of all trajectories from
denote a reachability tree, which encodes
the set of all trajectories from ![]() that can be obtained by
applying trajectories in
that can be obtained by
applying trajectories in
![]() . Each vertex of
. Each vertex of
![]() is a
reachable state,
is a
reachable state,
![]() . Each edge of
. Each edge of
![]() is
directed; its source represents a starting state, and its destination
represents the state obtained by applying a constant action
is
directed; its source represents a starting state, and its destination
represents the state obtained by applying a constant action ![]() over time
over time ![]() . Each edge
. Each edge ![]() represents an action
trajectory segment,
represents an action
trajectory segment,
![]() . This can be
transformed into a state trajectory,
. This can be
transformed into a state trajectory,
![]() , via integration using
(14.1), from 0 to
, via integration using
(14.1), from 0 to ![]() of
of ![]() from the
source state of
from the
source state of ![]() .
.
Thus, in terms of
![]() ,
, ![]() can be considered as a topological
graph in
can be considered as a topological
graph in ![]() (
(![]() will be used as an
abbreviation of
will be used as an
abbreviation of
![]() ). The swath
). The swath ![]() of
of ![]() is
is
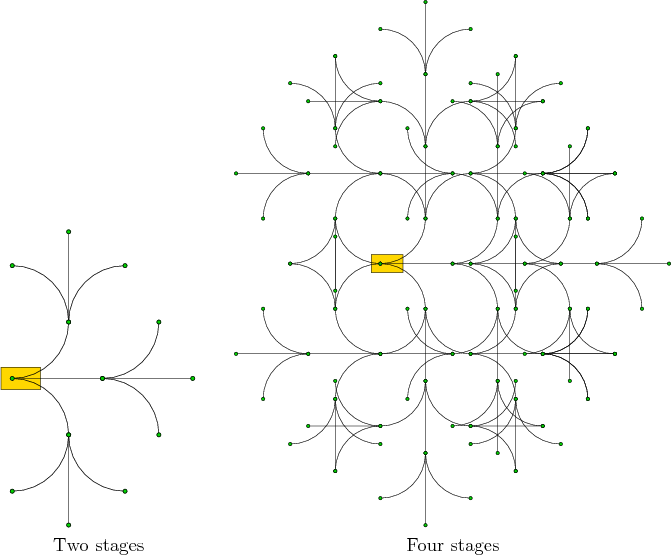 |
From Example 14.4 it can be seen that it is sometimes possible to arrive at the same state using two or more alternative action trajectories. Since each action trajectory can be expressed as an action sequence, the familiar issue arises from classical AI search of detecting whether the same state has been reached from different action sequences. For some systems, the reachability problem can be dramatically simplified by exploiting this information. If the same state is reached from multiple action sequences, then only one vertex needs to be represented.
This yields a directed reachability graph
![]() ,
which is obtained from
,
which is obtained from
![]() by merging its duplicate
states. If every action sequence arrives at a unique state, then the
reachability graph reduces to the reachability tree. However, if
multiple action sequences arrive at the same state, this is
represented as a single vertex
by merging its duplicate
states. If every action sequence arrives at a unique state, then the
reachability graph reduces to the reachability tree. However, if
multiple action sequences arrive at the same state, this is
represented as a single vertex
![]() . From this point onward,
the reachability graph will be primarily used. As for a reachability
tree, a reachability graph can be interpreted as a topological graph
in
. From this point onward,
the reachability graph will be primarily used. As for a reachability
tree, a reachability graph can be interpreted as a topological graph
in ![]() , and its swath
, and its swath
![]() is defined by adapting
(14.8).
is defined by adapting
(14.8).
The simplest case of arriving at the same state was observed in
Example 2.1. The discrete grid in the plane can be
modeled using the terminology of Chapter 13 as a system of
the form
![]() and
and
![]() for a state space
for a state space
![]() . The discretized set
. The discretized set ![]() of actions is
of actions is ![]() ,
, ![]() ,
,
![]() ,
, ![]() . Let
. Let
![]() . In this case, the
reachability graph becomes the familiar 2D grid. If
. In this case, the
reachability graph becomes the familiar 2D grid. If ![]() is the
initial state, then the grid vertices consist of all states in which
both coordinates are integers.
is the
initial state, then the grid vertices consist of all states in which
both coordinates are integers.
Through careless discretization of an arbitrary system, such a nice
grid usually does not arise. However, in many cases a discretization
can be carefully chosen so that the states become trapped on a grid or
lattice. This has some advantages in sampling-based planning.
Section 14.4.1 covers a method that exploits such structure
for the system
![]() . It can even be extended to more general
systems, provided that the system can be expressed as
. It can even be extended to more general
systems, provided that the system can be expressed as
![]() and it is not underactuated. It was shown recently that by a clever choice of
discretization, a very large class of nonholonomic
systems14.4 can
also be forced onto a lattice [762]. This is usually
difficult to achieve, and under most discretizations the vertices of
the reachability graph are dense in the reachable set.
and it is not underactuated. It was shown recently that by a clever choice of
discretization, a very large class of nonholonomic
systems14.4 can
also be forced onto a lattice [762]. This is usually
difficult to achieve, and under most discretizations the vertices of
the reachability graph are dense in the reachable set.
It is also possible to define backward versions of the reachability tree and reachability graph, in the same way that backward reachable sets were obtained. These indicate initial states and action sequences that will reach a given goal state and are no more difficult to define or compute than their forward counterparts. They might appear more difficult, but keep in mind that the initial states are not fixed; thus, no BVP appears. The initial states can be obtained by reverse-time integration of the state transition equation; see Section 14.3.2.
Steven M LaValle 2012-04-20