
Next: Multistep methods Up: 14.3.2 System Simulator Previous: Euler method
Although Euler integration is efficient and easy to understand, it
generally yields poor approximations. Taking a Taylor series
expansion of
![]() at
at ![]() yields
yields
Runge-Kutta methods are based on using higher order terms of the
Taylor series expansion. One of the most widely used and efficient
numerical integration methods is the fourth-order Runge-Kutta method.
It is simple to implement and yields good numerical behavior in most
applications. Also, it is generally recommended over Euler
integration. The technique can be derived by performing a Taylor
series expansion at
![]() . This state itself is
estimated in the approximation process.
. This state itself is
estimated in the approximation process.
The fourth-order Runge-Kutta integration method is
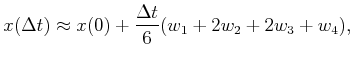 |
(14.18) |
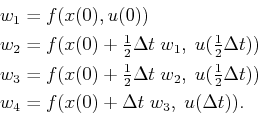 |
(14.19) |
The approximation error depends on how quickly higher order
derivatives of
![]() vary over time. This can be expressed using
the remaining terms of the Taylor series. In practice, it may be
advantageous to adapt
vary over time. This can be expressed using
the remaining terms of the Taylor series. In practice, it may be
advantageous to adapt ![]() over successive iterations of
Runge-Kutta integration. In [247], for example, it is
suggested that
over successive iterations of
Runge-Kutta integration. In [247], for example, it is
suggested that ![]() is scaled by
is scaled by
![]() ,
in which
,
in which
![]() , the Euclidean distance
in
, the Euclidean distance
in
![]() .
.
Steven M LaValle 2012-04-20