
Next: 14.3.4 General Framework Under Up: 14.3 Sampling-Based Motion Planning Previous: Reverse-time system simulation
The methods of Chapter 5 were based on the existence
of a local planning method (LPM) that is simple and efficient. This
represented an important part of both the incremental sampling and
searching framework of Section 5.4 and the
sampling-based roadmap framework of Section 5.6. In
the absence of obstacles and differential constraints, it is trivial
to define an LPM that connects two configurations. They can, for
example, be connected using the shortest path (geodesic) in ![]() . The
sampling-based roadmap approach from Section 5.6
relies on this simple LPM.
. The
sampling-based roadmap approach from Section 5.6
relies on this simple LPM.
In the presence of differential constraints, the problem of constructing an LPM that connects two configurations or states is considerably more challenging. Recall from Section 14.1 that this is the classical BVP, which is difficult to solve for most systems. There are two main alternatives to handle this difficulty in a sampling-based planning algorithm:
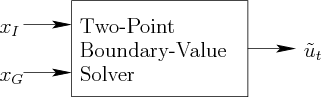 |
Under the first alternative, the BVP solver can be considered as a black box, as shown in Figure
14.10, that efficiently connects ![]() to
to ![]() in
the absence of obstacles. In the case of the Piano Mover's
Problem, this was obtained by moving along the shortest path in
in
the absence of obstacles. In the case of the Piano Mover's
Problem, this was obtained by moving along the shortest path in ![]() .
For many of the wheeled vehicle systems from Section
13.1.2, steering methods exist that could serve as an
efficient BVP solver; see Section 15.5. Efficient
techniques also exist for linear systems and are covered in Section
15.2.2.
.
For many of the wheeled vehicle systems from Section
13.1.2, steering methods exist that could serve as an
efficient BVP solver; see Section 15.5. Efficient
techniques also exist for linear systems and are covered in Section
15.2.2.
If the BVP is efficiently
solved, then virtually any sampling-based planning algorithm from
Chapter 5 can be adapted to the case of differential
constraints. This is achieved by using the module in Figure
14.10 as the LPM. For example, a sampling-based roadmap can
use the computed solution in the place of the shortest path through
![]() . If the BVP solver is
not efficient enough, then this approach becomes impractical because
it must typically be used thousands of times to build a roadmap. The
existence of an efficient module as shown in Figure 14.10
magically eliminates most of the complications associated with
planning under differential constraints. The only remaining concern
is that the solutions provided by the BVP solver could be quite long in comparison to
the shortest path in the absence of differential constraints (for
example, how far must the Dubins car travel to move slightly
backward?).
. If the BVP solver is
not efficient enough, then this approach becomes impractical because
it must typically be used thousands of times to build a roadmap. The
existence of an efficient module as shown in Figure 14.10
magically eliminates most of the complications associated with
planning under differential constraints. The only remaining concern
is that the solutions provided by the BVP solver could be quite long in comparison to
the shortest path in the absence of differential constraints (for
example, how far must the Dubins car travel to move slightly
backward?).
Under the second alternative, it is assumed that solving the BVP is very costly. The planning method in this case should avoid solving BVPs whenever possible. Some planning algorithms may only require an LPM that approximately reaches intermediate goal states, which is simpler for some systems. Other planning algorithms may not require the LPM to make any kind of connection. The LPM may return a motion primitive that appears to make some progress in the search but is not designed to connect to a prescribed state. This usually involves incremental planning methods, which are covered in Section 14.4 and extends the methods of Sections 5.4 and 5.5 to handle differential constraints.
Steven M LaValle 2012-04-20