
Next: Nonconvex polygons Up: 3.1.1 Polygonal and Polyhedral Previous: 3.1.1 Polygonal and Polyhedral
First consider ![]() for the case in which the obstacle region is a
convex, polygonal subset of a 2D world,
for the case in which the obstacle region is a
convex, polygonal subset of a 2D world,
![]() . A subset
. A subset
![]() is called convex if and only
if, for any pair of points in
is called convex if and only
if, for any pair of points in ![]() , all points along the line segment
that connects them are contained in
, all points along the line segment
that connects them are contained in ![]() . More precisely, this means
that for any
. More precisely, this means
that for any
![]() and
and
![]() ,
,
| (3.1) |
A boundary representation of ![]() is an
is an ![]() -sided polygon, which can
be described using two kinds of features: vertices and edges.
Every vertex corresponds to a ``corner'' of the polygon, and
every edge corresponds to a line segment between a pair of
vertices. The polygon can be specified by a sequence,
-sided polygon, which can
be described using two kinds of features: vertices and edges.
Every vertex corresponds to a ``corner'' of the polygon, and
every edge corresponds to a line segment between a pair of
vertices. The polygon can be specified by a sequence, ![]() ,
,
![]() ,
, ![]() ,
, ![]() , of
, of ![]() points in
points in
![]() , given in
counterclockwise order.
, given in
counterclockwise order.
A solid representation of ![]() can be expressed as the intersection of
can be expressed as the intersection of
![]() half-planes. Each half-plane corresponds to the set of all points
that lie to one side of a line that is common to a polygon edge.
Figure 3.1 shows an example of an octagon that is
represented as the intersection of eight half-planes.
half-planes. Each half-plane corresponds to the set of all points
that lie to one side of a line that is common to a polygon edge.
Figure 3.1 shows an example of an octagon that is
represented as the intersection of eight half-planes.
An edge of the polygon is specified by two points, such as ![]() and
and ![]() . Consider the equation of a line that passes through
. Consider the equation of a line that passes through
![]() and
and ![]() . An equation can be determined of the
form
. An equation can be determined of the
form
![]() , in which
, in which
![]() are constants that
are determined from
are constants that
are determined from ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Let
. Let
![]() be the function given by
be the function given by
![]() .
Note that
.
Note that
![]() on one side of the line, and
on one side of the line, and
![]() on
the other. (In fact,
on
the other. (In fact, ![]() may be interpreted as a signed Euclidean
distance from
may be interpreted as a signed Euclidean
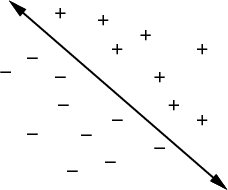
distance from ![]() to the line.) The sign of
to the line.) The sign of ![]() indicates a
half-plane that is bounded by the line, as depicted in Figure
3.2. Without loss of generality, assume that
indicates a
half-plane that is bounded by the line, as depicted in Figure
3.2. Without loss of generality, assume that ![]() is defined so that
is defined so that
![]() for all points to the left of the edge
from
for all points to the left of the edge
from ![]() to
to ![]() (if it is not, then multiply
(if it is not, then multiply ![]() by
by ![]() ).
).
 |
Let ![]() denote the
denote the ![]() function derived from the line that
corresponds to the edge from
function derived from the line that
corresponds to the edge from ![]() to
to
![]() for
for
![]() . Let
. Let ![]() denote the line equation that corresponds
to the edge from
denote the line equation that corresponds
to the edge from ![]() to
to ![]() . Let a half-plane
. Let a half-plane
![]() for
for
![]() be defined as a subset of
be defined as a subset of ![]() :
:
Steven M LaValle 2012-04-20