A distribution15.8 expresses a set of vector fields on a smooth manifold.
Suppose that a driftless control-affine system (15.53) is
given. Recall the vector space definition from Section
8.3.1 or from linear algebra. Also recall that a state
transition equation can be interpreted as a vector field if the
actions are fixed and as a vector space if the state is instead fixed.
For
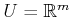 and a fixed
and a fixed 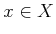 , the state transition equation
defines a vector space in which each
, the state transition equation
defines a vector space in which each 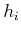 evaluated at
evaluated at  is a basis
vector and each
is a basis
vector and each 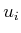 is a coefficient. For example, in
(15.54), the vector fields
is a coefficient. For example, in
(15.54), the vector fields 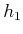 and
and 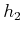 evaluated at
evaluated at
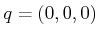 become
become
![$ [1 \;\; 0 \;\; 0]^T$](img6753.gif) and
and
![$ [0 \;\; 0 \;\; 1]^T$](img6754.gif) ,
respectively. These serve as the basis vectors. By selecting values
of
,
respectively. These serve as the basis vectors. By selecting values
of
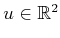 , a 2D vector space results. Any vector of the form
, a 2D vector space results. Any vector of the form
![$ [a \; \; 0 \;\; b]^T$](img6756.gif) can be represented by setting
can be represented by setting 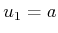 and
and
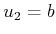 . More generally, let
. More generally, let
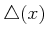 denote the vector space
obtained in this way for any
denote the vector space
obtained in this way for any 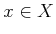 .
.
The dimension of a vector space is the number of independent basis
vectors. Therefore, the dimension of
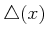 is the rank of
is the rank of
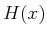 from (15.56) when evaluated at the particular
from (15.56) when evaluated at the particular 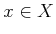 . Now consider defining
. Now consider defining
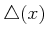 for every
for every 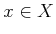 . This
yields a parameterized family of vector spaces, one for each
. This
yields a parameterized family of vector spaces, one for each 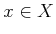 . The result could just as well be interpreted as a parameterized
family of vector fields. For example, consider actions for
. The result could just as well be interpreted as a parameterized
family of vector fields. For example, consider actions for 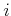 from
from
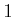 to
to 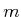 of the form
of the form 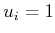 and
and 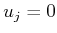 for all
for all
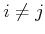 .
If the action is held constant over all
.
If the action is held constant over all 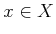 , then it selects a
single vector field
, then it selects a
single vector field 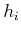 from the collection of
from the collection of 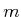 vector fields:
vector fields:
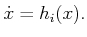 |
(15.63) |
Using constant actions, an 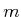 -dimensional vector space can be defined
in which each vector field
-dimensional vector space can be defined
in which each vector field 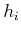 is a basis vector (assuming the
is a basis vector (assuming the
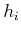 are linearly independent), and the
are linearly independent), and the
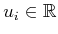 are the
coefficients:
are the
coefficients:
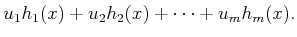 |
(15.64) |
This idea can be generalized to allow the 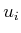 to vary over
to vary over 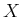 .
Thus, rather than having
.
Thus, rather than having 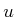 constant, it can be interpreted as a
feedback plan
constant, it can be interpreted as a
feedback plan
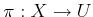 , in which the action at
, in which the action at  is given by
is given by
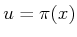 . The set of all vector fields that can be
obtained as
. The set of all vector fields that can be
obtained as
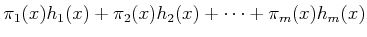 |
(15.65) |
is called the distribution of the set
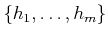 of
vector fields and is denoted as
of
vector fields and is denoted as
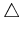 . If
. If
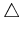 is obtained
from an control-affine system, then
is obtained
from an control-affine system, then
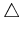 is called the system
distribution. The resulting set of vector
fields is not quite a vector space because the nonzero coefficients
is called the system
distribution. The resulting set of vector
fields is not quite a vector space because the nonzero coefficients
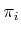 do not necessarily have a multiplicative inverse. This is
required for the coefficients of a vector field and was satisfied by
using
do not necessarily have a multiplicative inverse. This is
required for the coefficients of a vector field and was satisfied by
using
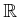 in the case of constant actions. A distribution is
instead considered algebraically as a module [469]. In
most circumstances, it is helpful to imagine it as a vector space
(just do not try to invert the coefficients!). Since a distribution
is almost a vector space, the
in the case of constant actions. A distribution is
instead considered algebraically as a module [469]. In
most circumstances, it is helpful to imagine it as a vector space
(just do not try to invert the coefficients!). Since a distribution
is almost a vector space, the
 notation from linear algebra is
often used to define it:
notation from linear algebra is
often used to define it:
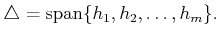 |
(15.66) |
Furthermore, it is actually a vector space with respect to
constant actions
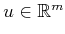 . Note that for each fixed
. Note that for each fixed 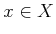 ,
the vector space
,
the vector space
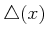 is obtained, as defined earlier. A
vector field
is obtained, as defined earlier. A
vector field 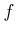 is said to belong to a distribution
is said to belong to a distribution
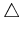 if it can be expressed using (15.65). If for all
if it can be expressed using (15.65). If for all 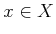 , the dimension of
, the dimension of
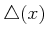 is
is 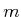 , then
, then
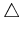 is called a
nonsingular distribution (or regular
distribution).
Otherwise,
is called a
nonsingular distribution (or regular
distribution).
Otherwise,
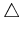 is called a singular
distribution, and the
points
is called a singular
distribution, and the
points 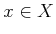 for which the dimension of
for which the dimension of
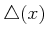 is less than
is less than
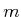 are called singular points. If the dimension of
are called singular points. If the dimension of
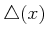 is a constant
is a constant 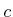 over all
over all 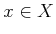 , then
, then 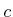 is called the dimension of the
distribution and is denoted by
is called the dimension of the
distribution and is denoted by
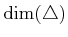 . If the vector fields
are smooth, and if
. If the vector fields
are smooth, and if 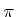 is restricted to be smooth, then a
smooth distribution is obtained, which is a subset of the
original distribution.
is restricted to be smooth, then a
smooth distribution is obtained, which is a subset of the
original distribution.
Figure 15.15:
The distribution
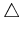 can be
imagined as a slice of the tangent bundle
can be
imagined as a slice of the tangent bundle 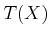 . It restricts the
tangent space at every
. It restricts the
tangent space at every 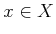 .
.
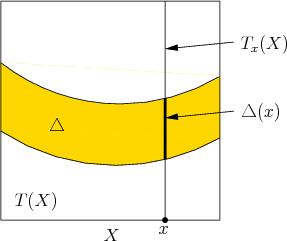 |
As depicted in Figure 15.15, a nice interpretation of
the distribution can be given in terms of the tangent bundle of a
smooth manifold. The tangent bundle was defined for
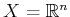 in (8.9) and generalizes to any smooth manifold
in (8.9) and generalizes to any smooth manifold 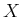 to obtain
to obtain
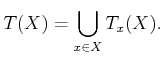 |
(15.67) |
The tangent bundle is a 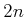 -dimensional manifold in which
-dimensional manifold in which 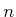 is the dimension of
is the dimension of 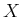 . A phase space for which
. A phase space for which
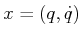 is
actually
is
actually
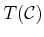 . In the current setting, each element of
. In the current setting, each element of 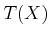 yields a state and a velocity,
yields a state and a velocity,
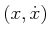 . Which pairs are possible
for a driftless control-affine system? Each
. Which pairs are possible
for a driftless control-affine system? Each
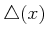 indicates the
set of possible
indicates the
set of possible 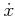 values for a fixed
values for a fixed  . The point
. The point  is
sometimes called the base and
is
sometimes called the base and
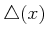 is called the fiber over
is called the fiber over
 in
in 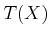 . The distribution
. The distribution
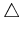 simply specifies a subset
of
simply specifies a subset
of 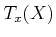 for every
for every 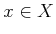 . For a vector field
. For a vector field 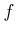 to belong to
to belong to
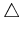 , it must satisfy
, it must satisfy
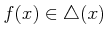 for all
for all 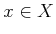 .
This is just a restriction to a subset of
.
This is just a restriction to a subset of 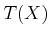 . If
. If 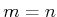 and the
system vector fields are independent, then any vector field is
allowed. In this case,
and the
system vector fields are independent, then any vector field is
allowed. In this case,
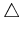 includes any vector field that can be
constructed from the vectors in
includes any vector field that can be
constructed from the vectors in 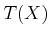 .
.
Example 15..7 (The Distribution for the Differential Drive)
The system in (
15.54) yields a two-dimensional
distribution:
![$\displaystyle {\triangle}= \operatorname{span}\{ [\cos\theta \;\; \sin\theta \;\; 0]^T, \; [0 \;\; 0 \;\; 1]^T\} .$](img6777.gif) |
(15.68) |
The distribution is nonsingular because for any
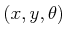
in the
coordinate neighborhood, the resulting vector space
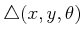
is two-dimensional.

Example 15..8 (A Singular Distribution)
Consider the following system, which is given in [
478]:
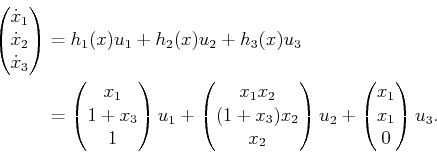 |
(15.69) |
The distribution is
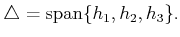 |
(15.70) |
The first issue is that for any
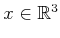
,
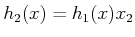
,
which implies that the vector fields are linearly dependent over all
of
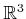
. Hence, this distribution is singular because
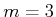
and
the dimension of
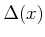
is
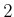
if
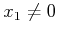
. If
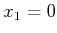
,
then the dimension of
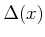
drops to
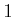
. The dimension of
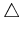
is not defined because the dimension of
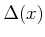
depends
on

.

A distribution can alternatively be defined directly from Pfaffian
constraints. Each
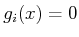 is called
an annihilator because enforcing the constraint eliminates many
vector fields from consideration. At each
is called
an annihilator because enforcing the constraint eliminates many
vector fields from consideration. At each 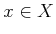 ,
,
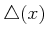 is
defined as the set of all velocity vectors that satisfy all
is
defined as the set of all velocity vectors that satisfy all 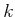 Pfaffian constraints. The constraints
themselves can be used to form a codistribution, which is a kind
of dual to the distribution. The codistribution can be interpreted as
a vector space in which each constraint is a basis vector.
Constraints can be added together or multiplied by any
Pfaffian constraints. The constraints
themselves can be used to form a codistribution, which is a kind
of dual to the distribution. The codistribution can be interpreted as
a vector space in which each constraint is a basis vector.
Constraints can be added together or multiplied by any
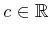 ,
and there is no effect on the resulting distribution of allowable
vector fields.
,
and there is no effect on the resulting distribution of allowable
vector fields.
Steven M LaValle
2012-04-20

![]() and a fixed
and a fixed ![]() , the state transition equation
defines a vector space in which each
, the state transition equation
defines a vector space in which each ![]() evaluated at
evaluated at ![]() is a basis
vector and each
is a basis
vector and each ![]() is a coefficient. For example, in
(15.54), the vector fields
is a coefficient. For example, in
(15.54), the vector fields ![]() and
and ![]() evaluated at
evaluated at
![]() become
become
![]() and
and
![]() ,
respectively. These serve as the basis vectors. By selecting values
of
,
respectively. These serve as the basis vectors. By selecting values
of
![]() , a 2D vector space results. Any vector of the form
, a 2D vector space results. Any vector of the form
![]() can be represented by setting
can be represented by setting ![]() and
and
![]() . More generally, let
. More generally, let
![]() denote the vector space
obtained in this way for any
denote the vector space
obtained in this way for any ![]() .
.
![]() is the rank of
is the rank of
![]() from (15.56) when evaluated at the particular
from (15.56) when evaluated at the particular ![]() . Now consider defining
. Now consider defining
![]() for every
for every ![]() . This
yields a parameterized family of vector spaces, one for each
. This
yields a parameterized family of vector spaces, one for each ![]() . The result could just as well be interpreted as a parameterized
family of vector fields. For example, consider actions for
. The result could just as well be interpreted as a parameterized
family of vector fields. For example, consider actions for ![]() from
from
![]() to
to ![]() of the form
of the form ![]() and
and ![]() for all
for all
![]() .
If the action is held constant over all
.
If the action is held constant over all ![]() , then it selects a
single vector field
, then it selects a
single vector field ![]() from the collection of
from the collection of ![]() vector fields:
vector fields:

![]() in (8.9) and generalizes to any smooth manifold
in (8.9) and generalizes to any smooth manifold ![]() to obtain
to obtain
![]() is called
an annihilator because enforcing the constraint eliminates many
vector fields from consideration. At each
is called
an annihilator because enforcing the constraint eliminates many
vector fields from consideration. At each ![]() ,
,
![]() is
defined as the set of all velocity vectors that satisfy all
is
defined as the set of all velocity vectors that satisfy all ![]() Pfaffian constraints. The constraints
themselves can be used to form a codistribution, which is a kind
of dual to the distribution. The codistribution can be interpreted as
a vector space in which each constraint is a basis vector.
Constraints can be added together or multiplied by any
Pfaffian constraints. The constraints
themselves can be used to form a codistribution, which is a kind
of dual to the distribution. The codistribution can be interpreted as
a vector space in which each constraint is a basis vector.
Constraints can be added together or multiplied by any
![]() ,
and there is no effect on the resulting distribution of allowable
vector fields.
,
and there is no effect on the resulting distribution of allowable
vector fields.