
Next: 15.4.3 Determining Controllability Up: 15.4.2 Determining Whether a Previous: 15.4.2.3 Lie brackets
The Lie bracket is the only tool needed to determine whether a system
is completely integrable (holonomic) or nonholonomic (not integrable).
Suppose that a system of the form (15.53) is given.
Using the ![]() system vector fields
system vector fields ![]() ,
, ![]() ,
, ![]() there are
there are
![]() Lie brackets of the form
Lie brackets of the form ![]() for
for ![]() that
can be formed. A distribution
that
can be formed. A distribution
![]() is called involutive [133] if for each of
these brackets there exist
is called involutive [133] if for each of
these brackets there exist ![]() coefficients
coefficients
![]() such that
such that
If the system is smooth and the distribution is nonsingular, then the Frobenius theorem immediately characterizes integrability:
A system is completely integrable if and only if it is involutive.Proofs of the Frobenius theorem appear in numerous differential geometry and control theory books [133,156,478,846]. There also exist versions that do not require the distribution to be nonsingular.
Determining integrability involves performing Lie brackets and
determining whether (15.86) is satisfied. The search for
the coefficients can luckily be avoided by using linear algebra tests
for linear independence. The
![]() matrix
matrix ![]() , which was
defined in (15.56), can be augmented into an
, which was
defined in (15.56), can be augmented into an
![]() matrix
matrix ![]() by adding
by adding ![]() as a new column. If the rank
of
as a new column. If the rank
of ![]() is
is ![]() for any pair
for any pair ![]() and
and ![]() , then it is
immediately known that the system is nonholonomic. If the rank of
, then it is
immediately known that the system is nonholonomic. If the rank of
![]() is
is ![]() for all Lie brackets, then the system is completely
integrable. Driftless linear systems, which are expressed as
for all Lie brackets, then the system is completely
integrable. Driftless linear systems, which are expressed as
![]() for a fixed matrix
for a fixed matrix ![]() , are completely integrable because all Lie
brackets are zero.
, are completely integrable because all Lie
brackets are zero.
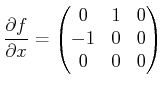 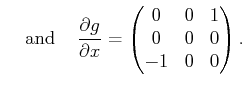 |
(15.90) |
The system can actually be constructed by differentiating the equation of a sphere. Let
| (15.93) |
Steven M LaValle 2012-04-20