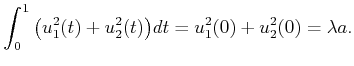The main idea of the method can be clearly illustrated for the
nonholonomic integrator,
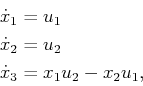 |
(15.146) |
which was considered throughout Section 15.5.1. This case
will be explained in detail, and the methods obtained by generalizing
the principles will subsequently be stated. The presentation given
here is based on [727,846].
As was previously indicated, growing independent vector fields as
quickly as possible is important. For the nonholonomic integrator,
![$ [h_1,h_2]$](img6893.gif) , is linearly independent of
, is linearly independent of 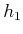 and
and 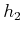 , as observed
in Example 15.12; thus, it satisfies this property.
Consider steering the system from some
, as observed
in Example 15.12; thus, it satisfies this property.
Consider steering the system from some
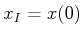 to some
to some
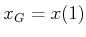 while optimizing the cost functional
while optimizing the cost functional
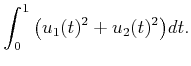 |
(15.147) |
The problem can be solved by using the constrained Lagrangian
formulation, which was given in Section 13.4.3. The first
step is to eliminate the 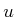 variables. From (15.146),
the cost can be expressed in terms of
variables. From (15.146),
the cost can be expressed in terms of
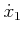 and
and
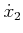 by using
by using
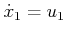 and
and
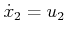 . The third equation in
(15.146) can be written as
. The third equation in
(15.146) can be written as
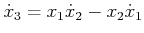 |
(15.148) |
and will be interpreted as a constraint on the Lagrangian, which is
combined using a (scalar) Lagrange multiplier as explained in Section
13.4.3. Define the Lagrangian as
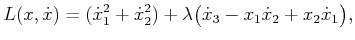 |
(15.149) |
in which the first term comes from the integrand of
(15.147), and the second term comes from
(15.148).
The Euler-Lagrange equation (13.118) yields
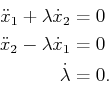 |
(15.150) |
Note that
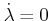 implies that
implies that
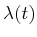 is constant for
all time. To obtain a differential equation that characterizes the
optimal action trajectory, use the fact that for
is constant for
all time. To obtain a differential equation that characterizes the
optimal action trajectory, use the fact that for 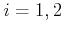 ,
,
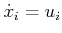 and
and
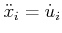 . This yields the equations
. This yields the equations
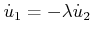 and
and
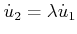 . These can be
represented as second-order linear differential equations. Based on
its roots, the solution is
. These can be
represented as second-order linear differential equations. Based on
its roots, the solution is
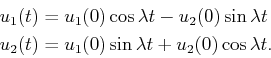 |
(15.151) |
Given initial and goal states, the optimal action trajectory is found
by determining 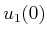 ,
, 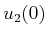 , and
, and 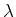 . Suppose that
. Suppose that
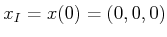 and
and
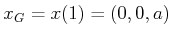 for some
for some
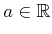 . Other cases can be obtained by applying transformations in
. Other cases can be obtained by applying transformations in
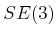 to the solution.
to the solution.
The state trajectories for 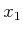 and
and 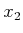 can be obtained by
integration of (15.151) because
can be obtained by
integration of (15.151) because
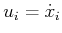 for
for 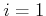 and
and 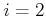 . Starting from
. Starting from
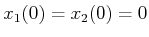 , this yields
, this yields
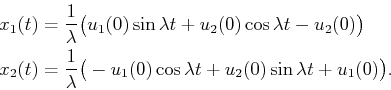 |
(15.152) |
To maintain the constraint that
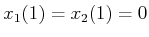 ,
, 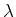 must
be chosen as
must
be chosen as
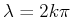 for some integer
for some integer 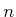 . Integration of
. Integration of
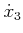 yields
yields
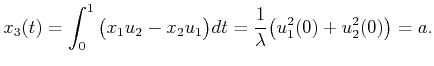 |
(15.153) |
The cost is
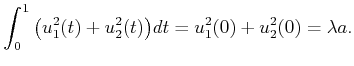 |
(15.154) |
The minimum cost is therefore achieved for 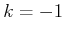 , which yields
, which yields
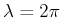 and
and
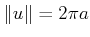 . This fixes the magnitude of
. This fixes the magnitude of
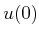 , but any direction may be chosen.
, but any direction may be chosen.
The steering problem can be solved in two phases:
- Apply any action trajectory to steer
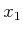 and
and 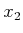 to their
desired values while neglecting to consider
to their
desired values while neglecting to consider 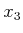 .
.
- Apply the solution just developed to steer
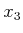 to the goal
while
to the goal
while 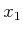 and
and 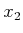 return to their values obtained in the first
phase.
return to their values obtained in the first
phase.
This idea can be generalized to other systems.
Steven M LaValle
2012-04-20

![]() , is linearly independent of
, is linearly independent of ![]() and
and ![]() , as observed
in Example 15.12; thus, it satisfies this property.
Consider steering the system from some
, as observed
in Example 15.12; thus, it satisfies this property.
Consider steering the system from some
![]() to some
to some
![]() while optimizing the cost functional
while optimizing the cost functional
![]() variables. From (15.146),
the cost can be expressed in terms of
variables. From (15.146),
the cost can be expressed in terms of
![]() and
and
![]() by using
by using
![]() and
and
![]() . The third equation in
(15.146) can be written as
. The third equation in
(15.146) can be written as
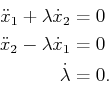
![]() and
and ![]() can be obtained by
integration of (15.151) because
can be obtained by
integration of (15.151) because
![]() for
for ![]() and
and ![]() . Starting from
. Starting from
![]() , this yields
, this yields