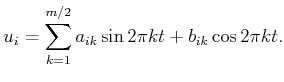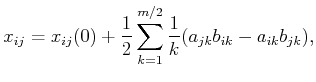The approach developed for the nonholonomic integrator generalizes to
systems of the form
and
Brockett showed in [142] that for such first-order
controllable systems, the optimal action trajectory is obtained by
applying a sum of sinusoids with integrally related frequencies for
each of the 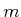 action variables. If
action variables. If 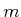 is even, then the trajectory
for each variable is a sum of
is even, then the trajectory
for each variable is a sum of 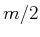 sinusoids at frequencies
sinusoids at frequencies 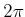 ,
,
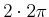 ,
, 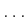 ,
,
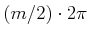 . If
. If 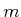 is odd, there are
instead
is odd, there are
instead 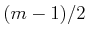 sinusoids; the sequence of frequencies remains the
same. Suppose
sinusoids; the sequence of frequencies remains the
same. Suppose 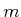 is even (the odd case is similar). Each action is
selected as
is even (the odd case is similar). Each action is
selected as
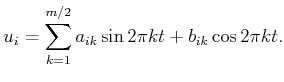 |
(15.157) |
The other state variables evolve as
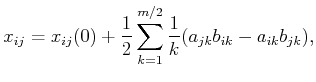 |
(15.158) |
which provides a constraint similar to (15.153). The
periodic behavior of these action trajectories causes the 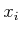 variables to return to their original values while steering the
variables to return to their original values while steering the
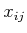 to their desired values. In a sense this is a vector-based
generalization in which the scalar case was the nonholonomic
integrator.
to their desired values. In a sense this is a vector-based
generalization in which the scalar case was the nonholonomic
integrator.
Once again, a two-phase steering approach is obtained:
- Apply any action trajectory that brings every
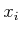 to its goal
value. The evolution of the
to its goal
value. The evolution of the 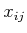 states is ignored in this stage.
states is ignored in this stage.
- Apply sinusoids of integrally related frequencies to the action
variables. Choose each
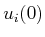 so that
so that 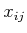 reaches its goal
value. In this stage, the
reaches its goal
value. In this stage, the 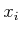 variables are ignored because they
will return to their values obtained in the first stage.
variables are ignored because they
will return to their values obtained in the first stage.
This method has been generalized even further to second-order
controllable systems:
in which 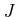 is the set of all unique triples formed from distinct
is the set of all unique triples formed from distinct
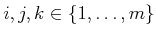 and removing unnecessary permutations due
to the Jacobi identity for Lie brackets. For this problem, a
three-phase steering method can be developed by using ideas similar to
the first-order controllable case. The first phase determines
and removing unnecessary permutations due
to the Jacobi identity for Lie brackets. For this problem, a
three-phase steering method can be developed by using ideas similar to
the first-order controllable case. The first phase determines 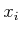 ,
the second handles
,
the second handles 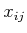 , and the third resolves
, and the third resolves 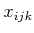 . See
[727,846] for more details.
. See
[727,846] for more details.
Steven M LaValle
2012-04-20