Lenses work because of Snell's law, which expresses how much rays of light bend when entering or exiting a transparent material. Recall that the speed of light in a medium is less than the speed  in an vacuum. For a given material, let its refractive index be defined as
in an vacuum. For a given material, let its refractive index be defined as
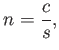 |
(4.2) |
in which 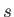 is the speed of light in the medium. For example,
is the speed of light in the medium. For example, 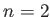 means that light takes twice as long to traverse the medium than through a vacuum. For some common examples,
means that light takes twice as long to traverse the medium than through a vacuum. For some common examples,
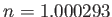 for air,
for air, 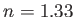 for water, and
for water, and 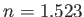 for crown glass.
for crown glass.
Figure:
Propagating wavefronts from a medium with low refractive index (such as air) to one with a higher index (such as glass). (a) The effect of slower propagation on the wavefronts is shown as they enter the lower medium. (b) This shows the resulting bending of a light ray, which is always perpendicular to the wavefronts. Snell's Law relates the refractive indices and angles as
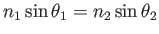 .
.
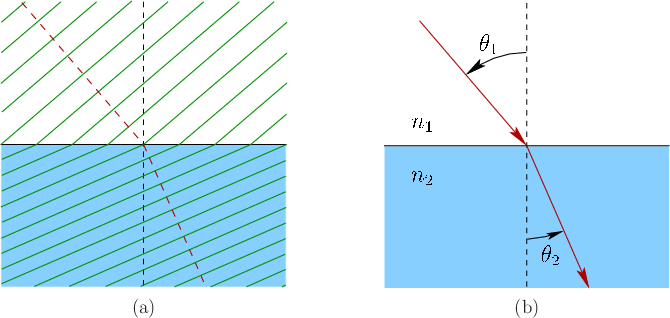 |
Figure 4.9 shows what happens to incoming light waves and rays. Suppose in this example that the light is traveling from air into glass, so that 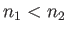 . Let
. Let 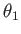 represent the incoming angle with respect to the surface normal, and let
represent the incoming angle with respect to the surface normal, and let 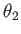 represent the resulting angle as it passes through the material. Snell's law relates the four quantities as
represent the resulting angle as it passes through the material. Snell's law relates the four quantities as
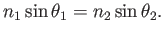 |
(4.3) |
Typically, 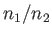 and
and 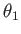 are given, so that (4.3) is solved for
are given, so that (4.3) is solved for 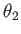 to obtain
to obtain
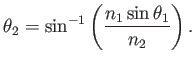 |
(4.4) |
If 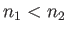 , then
, then 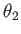 is closer to perpendicular than
is closer to perpendicular than 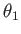 . If
. If 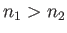 , then
, then 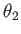 is further from perpendicular. The case of
is further from perpendicular. The case of 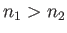 is also interesting in that light may not penetrate the surface if the incoming angle
is also interesting in that light may not penetrate the surface if the incoming angle 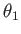 is too large. The range of
is too large. The range of 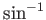 is 0 to
is 0 to 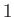 , which implies that (4.4) provides a solution for
, which implies that (4.4) provides a solution for 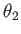 only if
only if
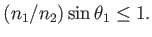 |
(4.5) |
If the condition above does not hold, then the light rays reflect from the surface. This situation occurs while under water and looking up at the surface. Rather than being able to see the world above, a swimmer might instead see a reflection, depending on the viewing angle.
Steven M LaValle
2020-01-06

![]() in an vacuum. For a given material, let its refractive index be defined as
in an vacuum. For a given material, let its refractive index be defined as

![]() . Let
. Let ![]() represent the incoming angle with respect to the surface normal, and let
represent the incoming angle with respect to the surface normal, and let ![]() represent the resulting angle as it passes through the material. Snell's law relates the four quantities as
represent the resulting angle as it passes through the material. Snell's law relates the four quantities as