
Next: How much field of Up: 5.4 Implications for VR Previous: How good does the Contents Index
We now address the spatial resolution. Insights into the required spatial
resolution are obtained from the photoreceptor densities. As was shown in
Figure 4.36, we see individual lights when a display is
highly magnified. As it is zoomed out, we may still perceive sharp
diagonal lines as being jagged, as shown in Figure
5.22(a); this phenomenon is known as aliasing.
Another artifact is the screen-door effect, shown in Figure
5.22(b); this is commonly noticed in an image produced
by a digital LCD projector. What does the display pixel density need
to be so that we do not perceive individual pixels? In 2010, Steve
Jobs of Apple Inc. claimed that ![]() pixels per linear inch (PPI) is enough, achieving what they called a retina display.5.1 Is this reasonable, and how does it relate to VR?
pixels per linear inch (PPI) is enough, achieving what they called a retina display.5.1 Is this reasonable, and how does it relate to VR?
 |
 |
Assume that the fovea is pointed directly at the display to provide the best sensing possible. The first issue is that red, green, and blue cones are arranged in a mosaic, as shown in Figure 5.23. The patterns are more erratic than the engineered versions in Figure 4.36. Vision scientists and neurobiologists have studied the effective or perceived input resolution through measures of visual acuity [141]. Subjects in a study are usually asked to indicate whether they can detect or recognize a particular target. In the case of detection, for example, scientists might like to know the smallest dot that can be perceived when printed onto a surface. In terms of displays, a similar question is: How small do pixels need to be so that a single white pixel against a black background is not detectable? In the case of recognition, a familiar example is attempting to read an eye chart, which displays arbitrary letters of various sizes. In terms of displays, this could correspond to trying to read text under various sizes, resolutions, and fonts. Many factors contribute to acuity tasks, such as brightness, contrast, eye movements, time exposure, and the part of the retina that is stimulated.
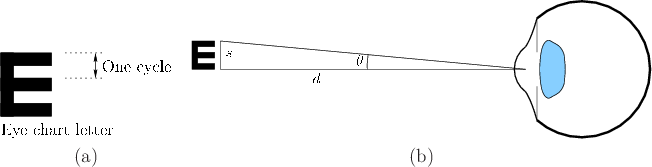
One of the most widely used concepts is cycles per degree, which roughly corresponds to the number of stripes (or sinusoidal peaks) that can be seen as separate along a viewing arc; see Figure 5.24. The Snellen eye chart, which is widely used by optometrists, is designed so that patients attempt to recognize printed letters from 20 feet away (or 6 meters). A person with ``normal'' 20/20 (or 6/6 in metric) vision is expected to barely make out the horizontal stripes in the letter ``E'' shown in Figure 5.24. This assumes he is looking directly at the letters, using the photoreceptors in the central fovea. The 20/20 line on the chart is designed so that letter height corresponds to ![]() cycles per degree when the eye is
cycles per degree when the eye is ![]() feet away. The total height of the ``E'' is
feet away. The total height of the ``E'' is ![]() of a degree. Note that each stripe is half of a cycle. What happens if the subject stands only
of a degree. Note that each stripe is half of a cycle. What happens if the subject stands only ![]() feet away from the eye chart? The letters should roughly appear to twice as large.
feet away from the eye chart? The letters should roughly appear to twice as large.
Using simple trigonometry,
We now return to the retina display concept. Suppose that a person with 20/20 vision is viewing a large screen that is ![]() feet (
feet (![]() m) away. To generate
m) away. To generate ![]() cycles per degree, it must have at least
cycles per degree, it must have at least ![]() pixels per degree. Using (5.1), the size would be
pixels per degree. Using (5.1), the size would be
![]() ft, which is equivalent to
ft, which is equivalent to ![]() in. Thus, only
in. Thus, only
![]() PPI would be sufficient. Now suppose that a smartphone screen is placed
PPI would be sufficient. Now suppose that a smartphone screen is placed ![]() inches from the user's eye. In this case,
inches from the user's eye. In this case,
![]() in. This requires that the screen have at least
in. This requires that the screen have at least
![]() PPI, which was satisfied by the
PPI, which was satisfied by the ![]() PPI originally claimed by Apple.
PPI originally claimed by Apple.
In the case of VR, the user is not looking directly at the screen as in the case of smartphones.
By inserting a lens for magnification, the display can be brought even closer to the eye. This is commonly done for VR headsets, as was shown in Figure 4.30. Suppose that the lens is positioned at its focal distance away from the screen, which for the sake of example is only ![]() in (this is comparable to current VR headsets). In this case,
in (this is comparable to current VR headsets). In this case,
![]() in, and the display must have at least
in, and the display must have at least ![]() PPI to achieve
PPI to achieve ![]() cycles per degree! One of the highest-density smartphone displays available today is in the Sony Xperia Z5 Premium. It has only
cycles per degree! One of the highest-density smartphone displays available today is in the Sony Xperia Z5 Premium. It has only ![]() PPI, which means that the PPI needs to increase by roughly a factor of three to obtain retina display resolution for VR headsets.
PPI, which means that the PPI needs to increase by roughly a factor of three to obtain retina display resolution for VR headsets.
This is not the complete story because some people, particularly youths, have better than 20/20 vision. The limits of visual acuity have been established to be around ![]() to
to ![]() cycles per degree, based on photoreceptor density and neural processes [38,52]; however, this is based on shining a laser directly onto the retina, which bypasses many optical aberration problems as the light passes through the eye. A small number of people (perhaps one percent) have acuity up to
cycles per degree, based on photoreceptor density and neural processes [38,52]; however, this is based on shining a laser directly onto the retina, which bypasses many optical aberration problems as the light passes through the eye. A small number of people (perhaps one percent) have acuity up to ![]() cycles per degree. In this extreme case, the display density would need to be
cycles per degree. In this extreme case, the display density would need to be ![]() PPI. Thus, many factors are involved in determining a sufficient resolution for VR. It suffices to say that the resolutions that exist today in consumer VR headsets are inadequate, and retinal display resolution will not be achieved until the PPI is several times higher.
PPI. Thus, many factors are involved in determining a sufficient resolution for VR. It suffices to say that the resolutions that exist today in consumer VR headsets are inadequate, and retinal display resolution will not be achieved until the PPI is several times higher.
Steven M LaValle 2020-01-06