Figure 7.4:
A bidirectional reflectance distribution function (BRDF), meticulously specifies the ratio of incoming and outgoing light energy for all possible perspectives.
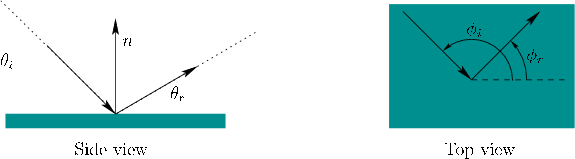 |
The shading models presented so far are in widespread use due to their simplicity and efficiency, even though they neglect most of the physics. To account for shading in a more precise and general way, a bidirectional reflectance distribution function (BRDF) is constructed [235]; see Figure 7.4. The 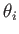 and
and 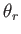 parameters represent the angles of light source and viewing ray, respectively, with respect to the surface. The
parameters represent the angles of light source and viewing ray, respectively, with respect to the surface. The 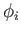 and
and 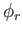 parameters range from 0 to
parameters range from 0 to 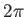 and represent the angles made by the light and viewing vectors when looking straight down on the surface (the vector
and represent the angles made by the light and viewing vectors when looking straight down on the surface (the vector 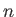 would point at your eye).
would point at your eye).
The BRDF is a function of the form
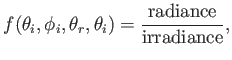 |
(7.7) |
in which radiance is the light energy reflected from the surface in directions 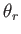 and
and 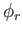 and irradiance is the light energy arriving at the surface from directions
and irradiance is the light energy arriving at the surface from directions 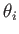 and
and 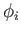 . These are expressed at a differential level, roughly corresponding to an infinitesimal surface patch. Informally, it is the ratio of the amount of outgoing light to the amount of incoming light at one point on the surface. The previous shading models can be expressed in terms of a simple BRDF. For Lambertian shading, the BRDF is constant because the surface reflects equally in all directions. The BRDF and its extensions can account for much more complex and physically correct lighting effects, with a wide variety of surface textures. See Chapter 7 of [5] for extensive coverage.
. These are expressed at a differential level, roughly corresponding to an infinitesimal surface patch. Informally, it is the ratio of the amount of outgoing light to the amount of incoming light at one point on the surface. The previous shading models can be expressed in terms of a simple BRDF. For Lambertian shading, the BRDF is constant because the surface reflects equally in all directions. The BRDF and its extensions can account for much more complex and physically correct lighting effects, with a wide variety of surface textures. See Chapter 7 of [5] for extensive coverage.
Steven M LaValle
2020-01-06


![]() and
and ![]() parameters represent the angles of light source and viewing ray, respectively, with respect to the surface. The
parameters represent the angles of light source and viewing ray, respectively, with respect to the surface. The ![]() and
and ![]() parameters range from 0 to
parameters range from 0 to ![]() and represent the angles made by the light and viewing vectors when looking straight down on the surface (the vector
and represent the angles made by the light and viewing vectors when looking straight down on the surface (the vector ![]() would point at your eye).
would point at your eye).