
Next: Mapping the surface Up: 7.2 Rasterization Previous: Depth buffer Contents Index
As each triangle is rendered, information from it is mapped from the virtual world onto the screen. This is usually accomplished using barycentric coordinates (see Figure 7.7), which expresses each point in the triangle interior as a weighted average of the three vertices:
| (7.10) |
The coordinates are calculated using Cramer's rule to solve a resulting linear system of equations. In particular, let
![]() for all combinations of
for all combinations of ![]() and
and ![]() . Furthermore, let
. Furthermore, let
| (7.11) |
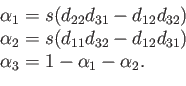 |
(7.12) |
Furthermore, given the barycentric coordinates, the test in (7.9) can be replaced by simply determining whether
![]() ,
,
![]() , and
, and
![]() . If any barycentric coordinate is less than zero, then
. If any barycentric coordinate is less than zero, then ![]() must lie outside of the triangle.
must lie outside of the triangle.
Steven M LaValle 2020-01-06