
Next: VR-specific rasterization problems Up: 7.2 Rasterization Previous: Aliasing Contents Index
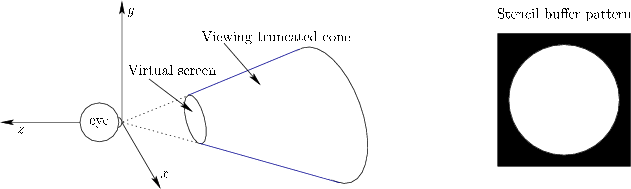 |
In practice, many triangles can be quickly eliminated before attempting to render them. This results in a preprocessing phase of the rendering approach called culling, which dramatically improves performance and enables faster frame rates. The efficiency of this operation depends heavily on the data structure used to represent the triangles. Thousands of triangles could be eliminated with a single comparison of coordinates if they are all arranged in a hierarchical structure. The most basic form of culling is called view volume culling, which eliminates all triangles that are wholly outside of the viewing frustum (recall Figure 3.18). For a VR headset, the frustum may have a curved cross section due to the limits of the optical system (see Figure 7.13). In this case, the frustum must be replaced with a region that has the appropriate shape. In the case of a truncated cone, a simple geometric test can quickly eliminate all objects outside of the view. For example, if
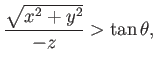 |
(7.14) |
Another form is called backface culling, which removes triangles that have outward surface normals that point away from the focal point. These should not be rendered ``from behind'' if the model is consistently formed. Additionally, occlusion culling may be used to eliminate parts of the model that might be hidden from view by a closer object. This can get complicated because it once again considers the depth ordering problem. For complete details, see [5].
Steven M LaValle 2020-01-06