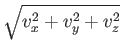Now consider the motion of a point in a 3D world
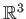 . Imagine that a geometric model, as defined in Section 3.1, is moving over time. This causes each point
. Imagine that a geometric model, as defined in Section 3.1, is moving over time. This causes each point 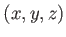 on the model to move, resulting a function of time for each coordinate of each point:
on the model to move, resulting a function of time for each coordinate of each point:
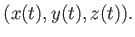 |
(8.8) |
The velocity 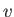 and acceleration
and acceleration 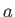 from Section 8.1.1 must therefore expand to have three coordinates. The velocity
from Section 8.1.1 must therefore expand to have three coordinates. The velocity 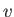 is replaced by
is replaced by
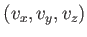 to indicate velocity with respect to the
to indicate velocity with respect to the 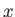 ,
, 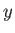 , and
, and 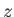 coordinates, respectively. The magnitude of
coordinates, respectively. The magnitude of 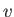 is called the speed:
is called the speed:
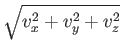 |
(8.9) |
Continuing further, the acceleration also expands to include three components:
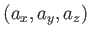 .
.
Steven M LaValle
2020-01-06